【题目】如图,抛物线![]() 经过原点,与
经过原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,将抛物线
,将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
, ![]() 交
交![]() 轴于
轴于![]() ,
, ![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),交
的左边),交![]() 轴于点
轴于点![]() .
.


(![]() )求抛物线
)求抛物线![]() 的解析式及顶点坐标.
的解析式及顶点坐标.
(![]() )以
)以![]() 为斜边向上作等腰直角三角形
为斜边向上作等腰直角三角形![]() ,当点
,当点![]() 落在抛物线
落在抛物线![]() 的对称轴上时,求抛物线
的对称轴上时,求抛物线![]() 的解析式.
的解析式.
(![]() )若抛物线
)若抛物线![]() 的对称轴存在点
的对称轴存在点![]() ,使
,使![]() 为等边三角形,请直接写出
为等边三角形,请直接写出![]() 的值.
的值.
参考答案:
【答案】(1)抛物线![]() 的解析式为
的解析式为![]() ,顶点坐标
,顶点坐标![]() ;
;
(2)抛物线![]() 的解析式为:
的解析式为: ![]() ;
;
(3)![]() .
.
【解析】试题分析:(1)把(0,0)及(2,0)代入y=x2+bx+c,求出抛物线C1的解析式,即可求出抛物线C1的顶点坐标;
(2)先求出C2的解析式,确定A,B,C的坐标,过点C作CH⊥对称轴DE,垂足为H,利用△PAC为等腰直角三角形,求出角的关系可证得△CHD≌△DEA,再由OC=EH列出方程求解得出m的值,即可得出C2的解析式.
(3)连接BC,BP,由抛物线对称性可知AP=BP,由△PAC为等边三角形,可得AP=BP=CP,∠APC=60°,由C,A,B三点在以点P为圆心,PA为半径的圆上,可得BC=2OC,利用勾股定理求出OB=![]() OC,列出方程求出m的值即可.
OC,列出方程求出m的值即可.
试题解析:解:(1)∵抛物线C1经过原点,与x轴的另一个交点为(2,0),∴![]() ,解得:
,解得: ![]() ,∴抛物线C1的解析式为y=x2﹣2x,∴抛物线C1的顶点坐标(1,﹣1);
,∴抛物线C1的解析式为y=x2﹣2x,∴抛物线C1的顶点坐标(1,﹣1);
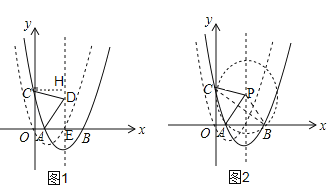
(2)如图1,∵抛物线C1向右平移m(m>0)个单位得到抛物线C2,∴C2的解析式为y=(x﹣m﹣1)2﹣1,∴A(m,0),B(m+2,0),C(0,m2+2m),过点C作CH⊥对称轴DE,垂足为H,∵△ACD为等腰直角三角形,∴AD=CD,∠ADC=90°,∴∠CDH+∠ADE=90°,∴∠HCD=∠ADE,∵∠DEA=90°,∴△CHD≌△DEA,∴AE=HD=1,CH=DE=m+1,∴EH=HD+DE=1+m+1=m+2,由OC=EH得m2+2m=m+2,解得m1=1,m2=﹣2(舍去),∴抛物线C2的解析式为:y=(x﹣2)2﹣1.
(3)如图2,连接BC,BP,由抛物线对称性可知AP=BP,∵△PAC为等边三角形,∴AP=BP=CP,∠APC=60°,∴C,A,B三点在以点P为圆心,PA为半径的圆上,∴∠CBO=![]() ∠CPA=30°,∴BC=2OC,∴由勾股定理得OB=
∠CPA=30°,∴BC=2OC,∴由勾股定理得OB=![]() =
=![]() OC,∴
OC,∴![]() (m2+2m)=m+2,解得m1=
(m2+2m)=m+2,解得m1=![]() ,m2=﹣2(舍去),∴m=
,m2=﹣2(舍去),∴m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明家小区空地上有两棵笔直的树
 、
、 .一天,他在
.一天,他在 处测得树顶
处测得树顶 的仰角
的仰角 ,在
,在 处测得树顶
处测得树顶 的仰角
的仰角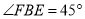 ,线段
,线段 恰好经过树顶
恰好经过树顶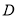 .已知.
.已知.  、
、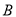 两处的距离为
两处的距离为 米,两棵树之间的距离
米,两棵树之间的距离 米,
米,  、
、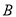 、
、 、
、 四点在一条直线上,求树
四点在一条直线上,求树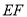 的高度.(
的高度.( ,
,  ,结果精确到
,结果精确到 )
)
-
科目: 来源: 题型:
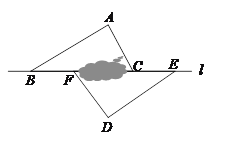
查看答案和解析>>【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在汕头市“创文”活动中,一项绿化工程由甲、乙两工程队承担.已知甲工程队单独完成这项工作需120天,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了
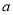 天完成,乙做另一部分用了
天完成,乙做另一部分用了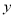 天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天?
天完成.若乙工程队还有其它工作任务,最多只能做52天.求甲工程队至少应做多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△ABC,
(2)再在图中画出△ABC的高CD,
(3)在右图中能使S△ABC=S△PBC的格点P的个数有 个(点P异于A)

-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个关于x的不等式,使-1,2都是它的解__________.
相关试题

