【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

参考答案:
【答案】(1)证明见解析;(2)∠AMB=α;(3)△CPQ为等腰直角三角形,证明见解析.
【解析】试题分析:(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CAD=∠CBE,再根据∠AFC=∠BFH,即可得到∠AMB=∠ACB=α;
(3)先根据SAS判定△ACP≌△BCQ,再根据全等三角形的性质,得出CP=CQ,∠ACP=∠BCQ,最后根据∠ACB=90°即可得到∠PCQ=90°,进而得到△PCQ为等腰直角三角形.
试题解析:(1)证明:如图①,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE.在△ACD和△BCE中,

∴△ACD≌△BCE(SAS),
∴BE=AD.
(2)解:如图①,∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠BAC+∠ABC=180°-α,
∴∠BAM+∠ABM=180°-α,
∴∠AMB=180°-(180°-α)=α.
(3)解:△CPQ为等腰直角三角形.
证明:如图②,由(1)可得,BE=AD.
∵AD,BE的中点分别为点P,Q,
∴AP=BQ.
∵△ACD≌△BCE,
∴∠CAP=∠CBQ.在△ACP和△BCQ中,
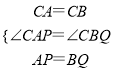
∴△ACP≌△BCQ(SAS),
∴CP=CQ且∠ACP=∠BCQ.
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察思考:如图,
 、
、 是直线
是直线 上的两个定点,点
上的两个定点,点 、
、 在直线
在直线 上运动(点
上运动(点 在点
在点 的左侧),
的左侧), ,已知
,已知 ,
,  、
、 间的距离为
间的距离为 ,连接
,连接 、
、 、
、 ,把
,把 沿
沿 折叠得
折叠得 .
.(
 )当
)当 、
、 两点重合时,则
两点重合时,则 __________
__________  .
.(
 )当
)当 、
、 两点不重合时,
两点不重合时,①连接
 ,探究
,探究 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.②若以
 、
、 、
、 、
、 为顶点的四边形是矩形,画出示意图并直接写出
为顶点的四边形是矩形,画出示意图并直接写出 的长.
的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解九年级学生的体能情况,随机抽取部分男生进行引体向上测试,并根据抽测成绩绘制成如下两幅统计图.


(
 )本次抽测的学生总人数为__________;请你补全图
)本次抽测的学生总人数为__________;请你补全图 的统计图.
的统计图.(
 )本次抽测成绩的众数为__________次;中位数为__________次.
)本次抽测成绩的众数为__________次;中位数为__________次.(
 )若规定引体向上
)若规定引体向上 次以上(含
次以上(含 次)为体能达到优秀,则该校
次)为体能达到优秀,则该校 名九年级男生中,估计有多少人能达到优秀?
名九年级男生中,估计有多少人能达到优秀? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
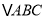 中,
中, 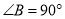 ,以
,以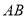 上的一点
上的一点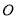 为圆心,以
为圆心,以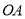 为半径的圆交
为半径的圆交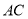 于点
于点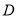 ,交
,交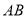 于点
于点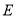 .
.
(
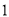 )求证:
)求证: 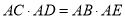 .
.(
 )如果
)如果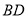 是⊙
是⊙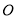 的切线,
的切线, 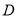 是切点,
是切点, 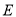 是
是 的中点,当
的中点,当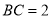 时,求
时,求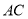 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明家小区空地上有两棵笔直的树
 、
、 .一天,他在
.一天,他在 处测得树顶
处测得树顶 的仰角
的仰角 ,在
,在 处测得树顶
处测得树顶 的仰角
的仰角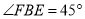 ,线段
,线段 恰好经过树顶
恰好经过树顶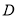 .已知.
.已知.  、
、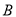 两处的距离为
两处的距离为 米,两棵树之间的距离
米,两棵树之间的距离 米,
米,  、
、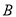 、
、 、
、 四点在一条直线上,求树
四点在一条直线上,求树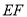 的高度.(
的高度.( ,
,  ,结果精确到
,结果精确到 )
)
-
科目: 来源: 题型:
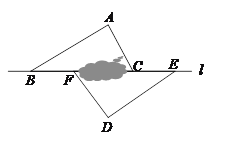
查看答案和解析>>【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 经过原点,与
经过原点,与 轴的另一个交点为
轴的另一个交点为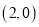 ,将抛物线
,将抛物线 向右平移
向右平移 个单位得到抛物线
个单位得到抛物线 ,
,  交
交 轴于
轴于 ,
,  两点(点
两点(点 在点
在点 的左边),交
的左边),交 轴于点
轴于点 .
.

(
 )求抛物线
)求抛物线 的解析式及顶点坐标.
的解析式及顶点坐标.(
 )以
)以 为斜边向上作等腰直角三角形
为斜边向上作等腰直角三角形 ,当点
,当点 落在抛物线
落在抛物线 的对称轴上时,求抛物线
的对称轴上时,求抛物线 的解析式.
的解析式.(
 )若抛物线
)若抛物线 的对称轴存在点
的对称轴存在点 ,使
,使 为等边三角形,请直接写出
为等边三角形,请直接写出 的值.
的值.
相关试题

