【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE. 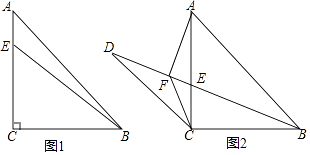
(1)如图1,若AB=4 ![]() ,BE=5,求AE的长;
,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.
参考答案:
【答案】
(1)解:∵∠ACB=90°,AC=BC,
∴AC=BC= ![]() AB=4,
AB=4,
∵BE=5,
∴CE= ![]() =3,
=3,
∴AE=4﹣3=1;
(2)解:∵∠ACB=90°,AC=BC,
∴∠CAB=45°,
∵AF⊥BD,
∴∠AFB=∠ACB=90°,
∴A,F,C,B四点共圆,
∴∠CFB=∠CAB=45°,
∴∠DFC=∠AFC=135°,
在△ACF与△DCF中, 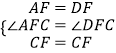 ,
,
∴△ACF≌△DCF,
∴CD=AC,
∵AC=BC,
∴AC=BC.
【解析】(1)根据等腰直角三角形的性质得到AC=BC= ![]() AB=4,根据勾股定理得到CE=
AB=4,根据勾股定理得到CE= ![]() =3,于是得到结论;(2)根据等腰直角三角形的性质得到∠CAB=45°,由于∠AFB=∠ACB=90°,推出A,F,C,B四点共圆,根据圆周角定理得到∠CFB=∠CAB=45°,求得∠DFC=∠AFC=135°,根据全等三角形的性质即可得到结论.
=3,于是得到结论;(2)根据等腰直角三角形的性质得到∠CAB=45°,由于∠AFB=∠ACB=90°,推出A,F,C,B四点共圆,根据圆周角定理得到∠CFB=∠CAB=45°,求得∠DFC=∠AFC=135°,根据全等三角形的性质即可得到结论.
【考点精析】关于本题考查的勾股定理的概念,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
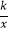 (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 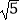 ,cos∠ACH=
,cos∠ACH=  ,点B的坐标为(4,n)
,点B的坐标为(4,n) 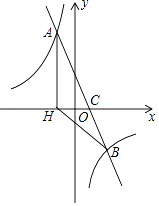
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表列出了国外几个城市与首都北京的时差(带正号的表示同一时刻比北京时间早的时数),如北京时间的上午10:00时,东京时间的10点已过去了1小时,现在已是10+1=11:00.

(1)如果现在是北京时间8:00,那么现在的纽约时间是多少;
(2)此时(北京时间8:00)小明想给远在巴黎姑妈打电话,你认为合适吗?为什么?
(3)如果现在是芝加哥时间上午6:00,那么现在北京时间是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小亮从家步行到公交车站台,乘公交车去学校. 图中的折线表示小亮的离家距离s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 公交车的速度是350m/min
C. 他步行的速度是100m/min D. 他等公交车时间为6min
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C.
 D.
D. 
-
科目: 来源: 题型:
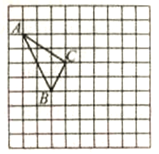
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为A(-4,5),C(-1,3).
(1)请在网格平面内作出平面直角坐标系(不写作法);
(2)请作出△ABC关于y轴对称△A'B'C';
(3)分别写出A'、B'、C'的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=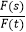 ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
相关试题

