【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
参考答案:
【答案】
(1)解:F(243)=(423+342+234)÷111=9;
F(617)=(167+716+671)÷111=14.
(2)解:∵s,t都是“相异数”,s=100x+32,t=150+y,
∴F(s)=(302+10x+230+x+100x+23)÷111=x+5,F(t)=(510+y+100y+51+105+10y)÷111=y+6.
∵F(t)+F(s)=18,
∴x+5+y+6=x+y+11=18,
∴x+y=7.
∵1≤x≤9,1≤y≤9,且x,y都是正整数,
∴ ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() .
.
∵s是“相异数”,
∴x≠2,x≠3.
∵t是“相异数”,
∴y≠1,y≠5.
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴k的最大值为 ![]() .
.
【解析】(1)根据F(n)的定义式,分别将n=243和n=617代入F(n)中,即可求出结论;(2)由s=100x+32、t=150+y结合F(s)+F(t)=18,即可得出关于x、y的二元一次方程,解之即可得出x、y的值,再根据“相异数”的定义结合F(n)的定义式,即可求出F(s)、F(t)的值,将其代入k= ![]() 中,找出最大值即可.
中,找出最大值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.
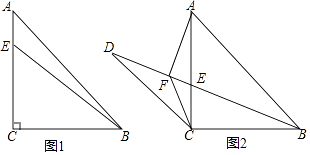
(1)如图1,若AB=4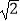 ,BE=5,求AE的长;
,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C.
 D.
D. 
-
科目: 来源: 题型:
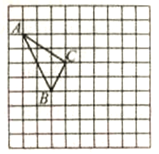
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为A(-4,5),C(-1,3).
(1)请在网格平面内作出平面直角坐标系(不写作法);
(2)请作出△ABC关于y轴对称△A'B'C';
(3)分别写出A'、B'、C'的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是____cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线
 射到平面镜
射到平面镜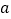 上,被
上,被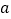 反射到平面镜
反射到平面镜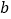 上,又被
上,又被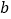 反射,若被
反射,若被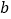 反射出的光线
反射出的光线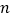 与光线
与光线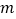 平行,且
平行,且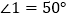 ,则
,则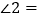 _________,
_________,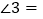 ________.
________.(2)在(1)中,若
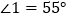 ,则
,则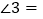 _______;若
_______;若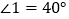 ,则
,则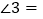 ________;
________;(3)由(1)、(2),请你猜想:当两平面镜
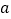 、
、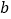 的夹角
的夹角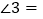 ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜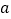 上的光线
上的光线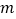 ,经过平面镜
,经过平面镜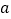 、
、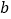 的两次反射后,入射光线
的两次反射后,入射光线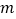 与反射光线
与反射光线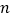 平行.请说明理由.
平行.请说明理由.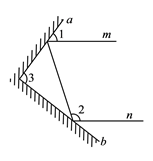
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:
第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
第九次
第十次
甲
7
10
8
10
9
9
10
8
10
9
乙
10
7
10
9
9
10
8
10
7
10
(1)选手甲的成绩的中位数是__________分;选手乙的成绩的众数是__________分;
(2)计算选手甲的平均成绩和方差;
(2)已知选手乙的成绩的方差是1.4,则成绩较稳定的是哪位选手?(直按写出结果)
相关试题

