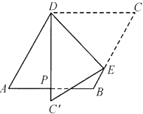
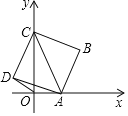
【题目】如图,菱形纸片![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边的中点,折叠纸片,使点
边的中点,折叠纸片,使点![]() 落在直线
落在直线![]() 上的
上的![]() 处,折痕为经过点
处,折痕为经过点![]() 的线段
的线段![]() .则
.则![]() 的度数为________.
的度数为________.
参考答案:
【答案】75°
【解析】
连接BD,可知△ABD是等边三角形,根据三线合一的性质得出DP平分∠ADB,即∠ADP=30°,再根据折叠性质可知,∠PDE=∠CDE=75°,然后根据三角形的内角和定理求出答案.
解:连接BD,
∵菱形![]() 中,
中,![]() ,
,
∴AD=AB,AB∥CD
∴△ABD是等边三角形,∠ADC=120°
∵PA=PB
∴∠ADP=∠BDP=30°
根据折叠的性质可知:∠PDE=∠CDE
∴∠CDE=(∠ADC-∠ADP) ÷2=(120°-30°)÷2=45°
∵∠CDE+∠C+![]() =180°
=180°
∴![]() =180°-(∠CDE+∠C)=180°-(45°+60°)=75°
=180°-(∠CDE+∠C)=180°-(45°+60°)=75°
故答案为:75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.
(1)1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)有46.4吨货物需要运输,货运公司拟安排大小货车共10辆(要求两种货车都要用),全部货物一次运完,其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且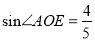 .
.(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,AB=2
 ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为
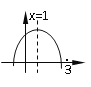
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是x轴上的一个动点,点C在y轴上,以AC为对角线画正方形ABCD,已知点C的坐标是
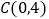 ,设点A的坐标为
,设点A的坐标为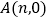 .
. 当
当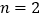 时,正方形ABCD的边长
时,正方形ABCD的边长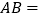 ______.
______.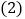 连结OD,当
连结OD,当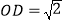 时,
时,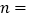 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,点
中,点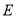 是
是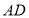 的中点,延长
的中点,延长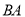 ,
,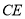 交于点
交于点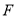 ,连结
,连结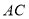 ,
,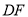 .
.(1)求证:四边形
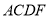 是平行四边形;
是平行四边形;(2)当
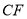 平分
平分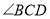 时,写出
时,写出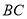 与
与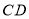 的数量关系,并说明理由.
的数量关系,并说明理由.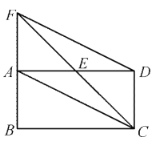
相关试题

