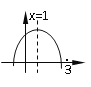
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】∵抛物线开口向下,∴a<0,∵抛物线对称轴为x=![]() =1,即b=﹣2a,∴b>0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,所以①错误;
=1,即b=﹣2a,∴b>0,∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,所以①错误;
∵b=﹣2a,∴2a+b=0,所以②正确;
∵x=1时,函数值最大,∴a+b+c>am2+bm+c,即a+b>am2+bm(m≠1),所以③正确;
∵抛物线与x轴的交点到对称轴x=1的距离大于1,∴抛物线与x轴的一个交点在点(2,0)与(3,0)之间,∴抛物线与x轴的另一个交点在点(0,0)与(﹣1,0)之间,∴x=﹣1时,y<0,∴a﹣b+c<0,所以④错误;
当ax12+bx1=ax22+bx2,则ax12+bx1+cax22+bx2+c,∴x=x1和x=x2所对应的函数值相等,∴x2﹣1=1﹣x1,∴x1+x2=2,所以⑤正确;
一共有3个正确,故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n)。线段OA=5,E为x轴上一点,且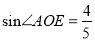 .
.(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,AB=2
 ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形纸片
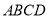 中,
中, ,点
,点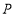 是
是 边的中点,折叠纸片,使点
边的中点,折叠纸片,使点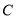 落在直线
落在直线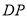 上的
上的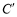 处,折痕为经过点
处,折痕为经过点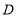 的线段
的线段 .则
.则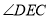 的度数为________.
的度数为________.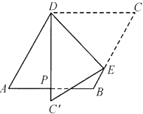
-
科目: 来源: 题型:
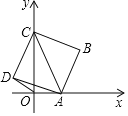
查看答案和解析>>【题目】如图,点A是x轴上的一个动点,点C在y轴上,以AC为对角线画正方形ABCD,已知点C的坐标是
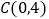 ,设点A的坐标为
,设点A的坐标为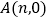 .
.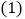 当
当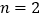 时,正方形ABCD的边长
时,正方形ABCD的边长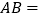 ______.
______. 连结OD,当
连结OD,当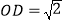 时,
时,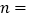 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,点
中,点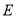 是
是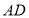 的中点,延长
的中点,延长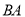 ,
,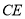 交于点
交于点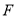 ,连结
,连结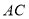 ,
,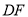 .
.(1)求证:四边形
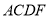 是平行四边形;
是平行四边形;(2)当
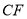 平分
平分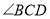 时,写出
时,写出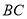 与
与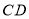 的数量关系,并说明理由.
的数量关系,并说明理由.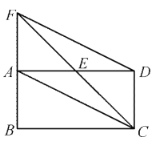
-
科目: 来源: 题型:
查看答案和解析>>【题目】信息化时代的到来,手机已经成为我们生活中不可缺少的一部分.为了解中学生在假期使用手机的情况(选项:
 .聊天;
.聊天; .游戏
.游戏 .学习;
.学习; .其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出).
.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出).
(1)这次被调查的学生有多少人?被调查的学生中,用手机学习的有多少人?
(2)将两个统计图补充完整;
(3)在扇形统计图中,请计算本项调查中用手机学习部分所对应的圆心角的度数;
(4)如果全校共1200名同学,请你估算用手机学习的学生人数.
相关试题

