【题目】如图,已知四边形ABCD为正方形,AB=2![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.

参考答案:
【答案】(1)、证明过程见解析;(2)、4;证明过程见解析;(3)、S==x2﹣4![]() x+8
x+8
【解析】
试题分析:(1)、作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEM≌△FEM,则有DE=EF即可;(2)、同(1)的方法判断出△ADE≌△CDG得到CG=AE,即:CE+CG=CE+AE=AC=4;(3)、由正方形的性质得到∠DAE=45°,表示出AM=EM,再表示出DM,再用勾股定理求出DE2.
试题解析:(1)、如图,作EM⊥BC,EN⊥CD
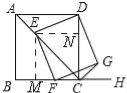
∴∠MEN=90°, ∵点E是正方形ABCD对角线上的点, ∴EM=EN, ∵∠DEF=90°, ∴∠DEN=∠MEF,
在△DEM和△FEM中,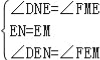 , ∴△DEM≌△FEM, ∴EF=DE, ∵四边形DEFG是矩形,
, ∴△DEM≌△FEM, ∴EF=DE, ∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)、CE+CG的值是定值,定值为4, ∵正方形DEFG和正方形ABCD, ∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°, ∴∠CDG=∠ADE, ∴△ADE≌△CDG,
∴AE=CE. ∴CE+CG=CE+AE=AC=![]() AB=
AB=![]() ×2
×2![]() =4,
=4,
(3)、如图,
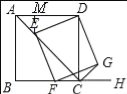
∵正方形ABCD中,AB=2![]() , ∴AC=4, 过点E作EM⊥AD,∴∠DAE=45°, ∵AE=x,
, ∴AC=4, 过点E作EM⊥AD,∴∠DAE=45°, ∵AE=x,
∴AM=EM=![]() x, 在Rt△DME中,DM=AD﹣AM=2
x, 在Rt△DME中,DM=AD﹣AM=2![]() ﹣
﹣![]() x,EM=
x,EM=![]() x,
x,
根据勾股定理得,DE2=DM2+EM2=(2![]() ﹣
﹣![]() x)2+(
x)2+(![]() x)2=x2﹣4
x)2=x2﹣4![]() x+8,
x+8,
∵四边形DEFG为正方形, ∴S=S正方形DEFG=DE2=x2﹣4![]() x+8.
x+8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天的最高气温是5℃,最低气温是﹣4℃,则这一天气温的温差是( )
A.1℃
B.﹣1℃
C.9℃
D.﹣9℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”:用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,随机被甲、乙、丙三人抢到.
(1)以下说法中正确的是
A.甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多
B.甲一定抢到金额最多的红包
C.乙一定抢到金额居中的红包
D.丙不一定抢到金额最少的红包
(2)记金额最多、居中、最少的红包分别为A,B,C,试求出甲抢到红包A的概率P(A).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个四边形中,如果有两个内角是直角,那么另外两个内角( ).
A. 都是钝角 B. 都是锐角
C. 一个是锐角,一个是直角 D. 互为补角
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则下列各式中正确的是( )
A.a﹣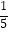 <b﹣
<b﹣ 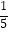
B.﹣4a>﹣4b
C.﹣2a+1<﹣2b+1
D.a2>b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】根据条件,求下列代数式的值:
(1)若
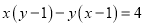 ,求
,求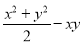 的值。
的值。(2)若
 求代数式
求代数式 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2017秒时,点P的坐标是( )
个单位长度,则第2017秒时,点P的坐标是( )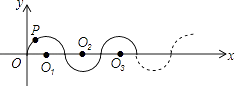
A.(2016,0)
B.(2017,1)
C.(2017,﹣1)
D.(2018,0)
相关试题

