【题目】在数轴上,四个不同的点![]() 分别表示有理数
分别表示有理数![]() ,且
,且![]() .
.
(1)如图1,![]() 为线段
为线段![]() 的中点,
的中点,

①当点![]() 与原点
与原点![]() 重合时,用等式表示
重合时,用等式表示![]() 与
与![]() 的关系为 ;
的关系为 ;
②求点![]() 表示的有理数
表示的有理数![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
(2)已知![]() ,
,
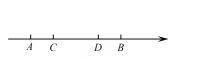
①若三点![]() 的位置如图所示,请在图中标出点
的位置如图所示,请在图中标出点![]() 的位置;
的位置;

②![]() 的大小关系为 (用“
的大小关系为 (用“![]() ”连接)
”连接)
参考答案:
【答案】(1)①![]() ,②
,②![]() ;(2)①见解析,②
;(2)①见解析,②![]() 或者
或者![]()
【解析】
(1) ①根据相反数的性质即可得出答案
②根据数轴上两点间的距离公式结合已知条件即可求得
(2) ①根据数轴上两点间的距离公式可得出AC=DB,从而确定点D的位置
②根据数轴上的点所表示的数,右边的总比左边的大即可得出答案
解:(1) ①∵![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 与原点
与原点![]() 重合
重合
∴![]()
![]() 为
为![]() 中点,
中点,
![]() .
.
![]() .
.
![]()
(2)①∵![]() ,
,![]() .
.
∴![]() ,∴AC=DB
,∴AC=DB
∴点![]() 的位置如图所示
的位置如图所示
②∵![]() ,∴
,∴![]() ,∴AC=DB
,∴AC=DB
如图 或
或![]()
∴![]() 或
或![]()
故答案为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则K的值不可能是( )
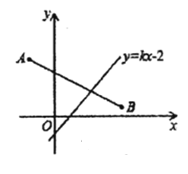
A. -5B. -2C. 3D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AM、BN分别与⊙O相切于点A、B,CD交AM、BN于点D、C,DO平分∠ADC.
(1)求证:CD是⊙O的切线;
(2)设AD=4,AB=x (x > 0),BC=y (y > 0). 求y关于x的函数解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
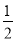 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
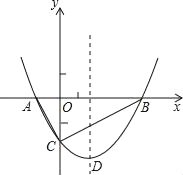
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)12-(-18)+(-5)-6;
(2)12÷(-
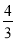 )×8;
)×8;(3)2-2÷(-
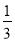 )×3;
)×3; (4)-12+
 ×(-2)3+ (-3)2;
×(-2)3+ (-3)2;(5)(-
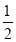 -
-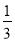 +
+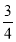 )×(-60).
)×(-60). -
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
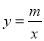 的图象如图所示,以下结论:
的图象如图所示,以下结论:①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.
其中正确的是( )
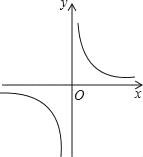
A. ①② B. ②③ C. ③④ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;⑤若
 的弦AB,CD交于点P,则
的弦AB,CD交于点P,则
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

