【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点后原路返校,如图为师生离校路程s与时间t之间的图象,请回答下列问题:
![]() 试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
![]() 如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.

参考答案:
【答案】(1)师生在13时36分回到学校;(2)见解析
【解析】试题分析:(1)先根据师生返校时的路程与时间之间的关系列出函数解析式,然后看图将两组对应s与t的值代入可得到一个二元一次方程组,解此方程组可得函数解析式.当返回学校时就是s为0时,t的值;
(2)先设符合学校要求的植树点与学校的路程为x(km),然后根据往返的平均速度、路程和时间得到一个不等式,解此不等式可得到x的取值范围,再确定植树点是否符合要求.
试题解析: ![]() 设师生返校时的函数解析式为
设师生返校时的函数解析式为![]() ,
,
如图所示,把![]() 、
、![]() 代入上式中得:
代入上式中得:
![]() ,
,
解此方程组得, ![]() ,
,
故![]() ,
,
当![]() 时,
时, ![]() ,
,
![]() 时36分
时36分
则师生在13时36分回到学校;
![]() 设符合学校要求的植树点与学校的路程为
设符合学校要求的植树点与学校的路程为![]() ,
,
由题意得: ![]() ,
,
解得: ![]() ,
,
![]() 、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,
、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,
![]() ,
,
答:13km,15km,17km植树点符合学校的要求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
240
180
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2.

A. 1275 B. 2500 C. 1225 D. 1250
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,则∠1+∠2=°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在
 两仓库分别有机器16台和12台,现要运往甲、乙两地,其中甲地需要15台,乙地需要13台,已知
两仓库分别有机器16台和12台,现要运往甲、乙两地,其中甲地需要15台,乙地需要13台,已知 两地仓库运往甲,乙两地机器的费用如下面的左表所示.
两地仓库运往甲,乙两地机器的费用如下面的左表所示. 设从A仓库调x台机器去甲地,请用含x的代数式补全下面的右表;
设从A仓库调x台机器去甲地,请用含x的代数式补全下面的右表;机器调运费用表机器调运方案表
出发地
目的地运费
 台
台 元
元
A
B
出发地
目的地机器
 台
台
A
B
合计
甲
500
300
甲地
x
15
乙
400
600
乙地
13
合计
16
12
28
 设总运费为y元,求y与x之间的函数解析式,并写出自变量x的取值范围;
设总运费为y元,求y与x之间的函数解析式,并写出自变量x的取值范围; 由机器调运方案表可知共有n种调运方案,求n的值.
由机器调运方案表可知共有n种调运方案,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)
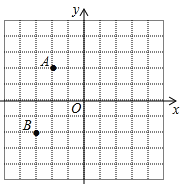
(1)若点D与点A关于y轴对称,则点D的坐标为 .
(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为 .
(3)求A,B,C,D组成的四边形ABCD的面积。
相关试题

