【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)
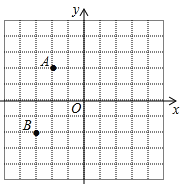
(1)若点D与点A关于y轴对称,则点D的坐标为 .
(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为 .
(3)求A,B,C,D组成的四边形ABCD的面积。
参考答案:
【答案】(1)(2,2);()2)(2,1);(3)![]() .
.
【解析】
试题分析:(1)根据关于y轴对称的点,纵坐标相同,横坐标互为相反数,可得答案;
(2)根据点向右平移加,向上平移加,可得答案;
(3)根据图形割补法,可得矩形BFDE,根据面积的和差,可得答案.
试题解析:(1)若点D与点A关于y轴对称,则点D的坐标为 (2,2);
(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为(2,1);
(3)如图
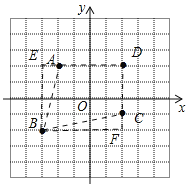 ,
,
S四边形ABCD=S矩形BFDE-S△ABE-S△BCF=5×4-![]() ×1×4-
×1×4-![]() ×1×5=
×1×5=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班师生组织植树活动,上午8时从学校出发,到植树地点后原路返校,如图为师生离校路程s与时间t之间的图象,请回答下列问题:
 试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校;
试写出师生返校时的s与t的函数关系式,并求出师生何时回到学校; 如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
如果师生骑自行车上午8时出发,到植树地点后,植树需2小时,要求14时前返回到学校,往返平均速度分别为每时10km、8km,现有A、B、C、D四个植树点与学校的路程分别是13km、15km、17km、19km,试通过计算说明哪几个植树点符合要求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠C=72°,∠D=81°.沿EF折叠四边形,使点A、B分别落在四边形内部的点A′、B′处,则∠1+∠2=°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在
 两仓库分别有机器16台和12台,现要运往甲、乙两地,其中甲地需要15台,乙地需要13台,已知
两仓库分别有机器16台和12台,现要运往甲、乙两地,其中甲地需要15台,乙地需要13台,已知 两地仓库运往甲,乙两地机器的费用如下面的左表所示.
两地仓库运往甲,乙两地机器的费用如下面的左表所示. 设从A仓库调x台机器去甲地,请用含x的代数式补全下面的右表;
设从A仓库调x台机器去甲地,请用含x的代数式补全下面的右表;机器调运费用表机器调运方案表
出发地
目的地运费
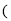 台
台 元
元
A
B
出发地
目的地机器
 台
台
A
B
合计
甲
500
300
甲地
x
15
乙
400
600
乙地
13
合计
16
12
28
 设总运费为y元,求y与x之间的函数解析式,并写出自变量x的取值范围;
设总运费为y元,求y与x之间的函数解析式,并写出自变量x的取值范围; 由机器调运方案表可知共有n种调运方案,求n的值.
由机器调运方案表可知共有n种调运方案,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,
 的圆心坐标为
的圆心坐标为 ,半径为
,半径为 函数
函数 的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点. 连接CO,求证:
连接CO,求证:  ;
; 若
若 是等腰三角形,求点P的坐标;
是等腰三角形,求点P的坐标; 当直线PO与
当直线PO与 相切时,求
相切时,求 的度数;当直线PO与
的度数;当直线PO与 相交时,设交点为E、F,点M为线段EF的中点,令
相交时,设交点为E、F,点M为线段EF的中点,令 ,求s与t之间的函数关系,并写出t的取值范围.
,求s与t之间的函数关系,并写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1 , 四边形EFQP的面积为S2 , 四边形PQCB的面积为S3 .

(1)求证:EF+PQ=BC;
(2)若S1+S3=S2 , 求 的值;
的值;
(3)若S3﹣S1=S2 , 直接写出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

相关试题

