搜索
【题目】已知二次函数y=ax2+bx+c（a≠0），其中自变量x与函数值y之间满足下面的对应关系：
x | …… | 3 | 5 | 7 | …… |
y | …… | 3.5 | 3.5 | -2 | …… |
则a+b+c=______．
参考答案：
【答案】-2
【解析】
利用表中数据和抛物线的对称性得到抛物线的对称轴为直线x=4，则可判断当x=1和x=7时函数值相等，所以x=1时，y=-2，然后把x=1时，y=-2代入解析式即可得到a+b+c的值．
∵x=3，y=3.5；x=5，y=3.5，
∴抛物线的对称轴为直线x=4，
∴当x=1和x=7时函数值相等，
而x=7时，y=-2，
∴x=1时，y=-2，
即a+b+c=-2．
故答案为：-2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，矩形ABCD中，AB=6，BD=10．Rt△EFG的直角边GE在CB的延长线上，E点与矩形的B点重合，∠FGE=90°，已知GE+AB=BC，FG=2GE．将矩形ABCD固定，把Rt△EFG沿着射线BC方向按每秒1个单位运动，直到点G到达点C停止运动．设Rt△EFG的运动时间为t秒（t＞0）．
（1）求出线段FG的长，并求出当点F恰好经过BD时，运动时间t的值；
（2）在整个运动过程中，设Rt△EFG与△BCD的重合部分面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】大双，小双的妈妈申购到一张北京奥运会的门票，兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球，各自设计一种游戏确定谁去．
大双：A袋中放着分别标有数字1，2，3的三个小球，B袋中放着分别标有数字4，5的两个小球，且都已各自搅匀，小双蒙上眼睛从两个口袋中各取出1个小球，若两个小球上的数字之积为偶数，则大双得到门票；若积为奇数，则小双得到门票．
小双：口袋中放着分别标有数字1，2，3的三个小球，且已搅匀，大双，小双各蒙上眼睛有放回地摸1次，大双摸到偶数就记2分，摸到奇数记0分；小双摸到奇数就记1分，摸到偶数记0分，积分多的就得到门票．（若积分相同，则重复第二次．）
（1）大双设计的游戏方案对双方是否公平？请你运用列表或树状图说明理由；
（2）小双设计的游戏方案对双方是否公平？不必说理．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=2x+2与y轴交于A点，与反比例函数y=
（x＞0）的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO=2．（1）求k的值；
（2）点N（a，1）是反比例函数y=
（x＞0）图象上的点，在x轴上是否存在点P，使得PM+PN最小？若存在，求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读解题过程，回答问题． 如图，OC在∠AOB内，∠AOB和∠COD都是直角，且∠BOC=30°，求∠AOD的度数．
解：过O点作射线OM，使点M，O，A在同一直线上．
因为∠MOD+∠BOD=90°，∠BOC+∠BOD=90°，
所以∠BOC=∠MOD，
所以∠AOD=180°﹣∠BOC=180°﹣30°=150°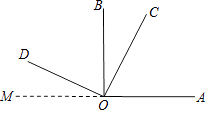
（1）如果∠BOC=60°，那么∠AOD等于多少度？如果∠BOC=n°，那么∠AOD等于多少度？
（2）如果∠AOB=∠DOC=x°，∠AOD=y°，求∠BOC的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】当实数m满足______条件时，一元二次方程x2-2x-m=0有两个不相等的实数根．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在﹣3，﹣1，0，1这四个数中，最小的数是（ ）
A. ﹣3B. ﹣1C. 0D. 1
相关试题
