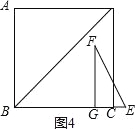
【题目】如图所示,矩形ABCD中,AB=6,BD=10.Rt△EFG的直角边GE在CB的延长线上,E点与矩形的B点重合,∠FGE=90°,已知GE+AB=BC,FG=2GE.将矩形ABCD固定,把Rt△EFG沿着射线BC方向按每秒1个单位运动,直到点G到达点C停止运动.设Rt△EFG的运动时间为t秒(t>0).
(1)求出线段FG的长,并求出当点F恰好经过BD时,运动时间t的值;
(2)在整个运动过程中,设Rt△EFG与△BCD的重合部分面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围.

参考答案:
【答案】(1)FG=4,t=![]() ;(2)S=
;(2)S=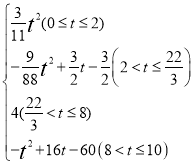 .
.
【解析】
试题分析:(1)利用矩形的性质和勾股定理易得FG,利用相似三角形的性质可得BG的长,进而可求出t的值;(2)①如图1,当0<t≤2时,根据三角形的面积公式求得结论;②如图2,当2<t≤![]() 时,根据三角形的面积公式即可得到结论;③如图3,当
时,根据三角形的面积公式即可得到结论;③如图3,当![]() <t≤8时,S=4④当8<t≤10时根据两三角形的面积差即可得到结论.
<t≤8时,S=4④当8<t≤10时根据两三角形的面积差即可得到结论.
试题解析:(1)在矩形ABCD中,AB=6,BD=10,∴由勾股定理得:BC=8,∵在Rt△EFG中,GE+AB=BC,FG=2GE.∴FG=4 ,当点F恰好经过BD时,∵∠FGE=90°,∠C=90°,∴FG∥DC,∴△BFG∽△BCD,∴![]() ,∴BG=
,∴BG=![]() ,∴BE=
,∴BE=![]() ,∴当点F恰好经过BD时,t=
,∴当点F恰好经过BD时,t=![]() .(2)①当0≤t≤2时,如图1,∵MN∥CD,∴三角形BMN相似三角形BCD,三角形MNE相似三角形FGE,设MN=x,则BN=
.(2)①当0≤t≤2时,如图1,∵MN∥CD,∴三角形BMN相似三角形BCD,三角形MNE相似三角形FGE,设MN=x,则BN=![]() ,NE=0.5x,则BE=
,NE=0.5x,则BE=![]() x=t,∴MN=
x=t,∴MN=![]() ,S=
,S=![]() t2,
t2,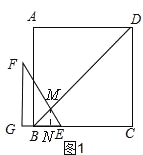 ②当2<t≤
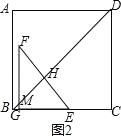
②当2<t≤![]() 时,如图2,S=﹣
时,如图2,S=﹣![]() t2+
t2+![]() t﹣
t﹣![]() ,
,
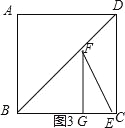
 ③当
③当![]() <t≤8时,如图3,S=4,
<t≤8时,如图3,S=4,
 ④当8<t≤10时,如图4,S=﹣t2+16t﹣60,
④当8<t≤10时,如图4,S=﹣t2+16t﹣60,
 ,综上可知S与t之间的函数关系式为:S=
,综上可知S与t之间的函数关系式为:S=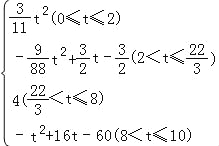 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )
A. 平均数B. 方差C. 中位数D. 极差
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列一元二次方程:
(1)x2-2x=0;
(2)16x2-9=0;
(3)4x2=4x-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
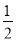 x与双曲线y=
x与双曲线y=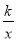 (k>0)交于A,B两点,且点A的横坐标为4.点C是双曲线上一点,且纵坐标为8,则△AOC的面积为( )
(k>0)交于A,B两点,且点A的横坐标为4.点C是双曲线上一点,且纵坐标为8,则△AOC的面积为( )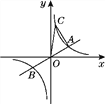
A. 8 B. 32 C. 10 D. 15
-
科目: 来源: 题型:
查看答案和解析>>【题目】大双,小双的妈妈申购到一张北京奥运会的门票,兄弟俩决定分别用标有数字且除数字以外没有其它任何区别的小球,各自设计一种游戏确定谁去.
大双:A袋中放着分别标有数字1,2,3的三个小球,B袋中放着分别标有数字4,5的两个小球,且都已各自搅匀,小双蒙上眼睛从两个口袋中各取出1个小球,若两个小球上的数字之积为偶数,则大双得到门票;若积为奇数,则小双得到门票.
小双:口袋中放着分别标有数字1,2,3的三个小球,且已搅匀,大双,小双各蒙上眼睛有放回地摸1次,大双摸到偶数就记2分,摸到奇数记0分;小双摸到奇数就记1分,摸到偶数记0分,积分多的就得到门票.(若积分相同,则重复第二次.)
(1)大双设计的游戏方案对双方是否公平?请你运用列表或树状图说明理由;
(2)小双设计的游戏方案对双方是否公平?不必说理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=
 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.(1)求k的值;
(2)点N(a,1)是反比例函数y=
 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0),其中自变量x与函数值y之间满足下面的对应关系:
x
……
3
5
7
……
y
……
3.5
3.5
-2
……
则a+b+c=______.
相关试题

