【题目】方程x2+4x﹣ ![]() +1=0的正数根的取值范围是( )
+1=0的正数根的取值范围是( )
A.0<x<1
B.1<x<2
C.2<x<3
D.3<x<4
参考答案:
【答案】B
【解析】解:方程x2+4x﹣ ![]() +1=0的正数根可看成函数y1=x2+4x+1与函数y2=
+1=0的正数根可看成函数y1=x2+4x+1与函数y2= ![]() (x>0)的交点.
(x>0)的交点.
画出两函数的图象,如图所示.

当x=1时,y1=12+4×1+1=6,y2= ![]() =10,
=10,
∴此时函数y2= ![]() 的图象在函数y1=x2+4x+1的上方;
的图象在函数y1=x2+4x+1的上方;
当x=2时,y1=22+4×2+1=13,y2= ![]() =5,
=5,
∴此时函数y2= ![]() 的图象在函数y1=x2+4x+1的下方.
的图象在函数y1=x2+4x+1的下方.
∴函数y1=x2+4x+1与函数y2= ![]() (x>0)的交点的横坐标1<x<2.
(x>0)的交点的横坐标1<x<2.
故B符合题意.
所以答案是:B.
【考点精析】解答此题的关键在于理解反比例函数的图象的相关知识,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点,以及对二次函数的图象的理解,了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)12-(-18)+(-7);
(2)12×(
 -
- +
+ )
)(3)8÷(-
 )×(-1
)×(-1 )+(-6);
)+(-6);(4)22-(1-
 )×|3-(-3)2|
)×|3-(-3)2| -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC和△DBE均为等腰直角三角形.
(1)求证:AD=CE;
(2)求证:AD和CE垂直.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备
 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.A型
B型
价格
 万元
万元 台
台
a
b
处理污水量
 吨
吨 月
月
240
200
 求a,b的值;
求a,b的值; 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案; 在
在 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
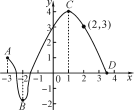
查看答案和解析>>【题目】已知两个变量x,y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出y的变化范围;
(2)求当x=0,-3时,y的对应值;
(3)求当y=0,3时,对应的x的值;
(4)当x为何值时,y的值最大?
(5)当x在什么范围内时,y的值在不断增加?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如下三个函数图象中,有两个函数图象能近似地刻画如下
 两个情境:
两个情境:
情境
 :小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;情境
 :小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.(1)情境
 ,
,  所对应的函数图象分别为 , (填写序号).
所对应的函数图象分别为 , (填写序号).(2)请你为剩下的函数图象写出一个适合的情境.
相关试题

