【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
参考答案:
【答案】(1)依题意得:![]()
解之得:![]()
(2)设购买A型设备x台,购买B型设备(10-x)台,
依题意得:12x+10(10-x)≤105
x≤2.5
所以该公司共有三种购买方案:
方案一,A型设备0台,B型设备10台
方案二,A型设备1台,B型设备9台
方案三,A型设备2台,B型设备8台
(3)在(2)问条件下,若要每月处理污水量不低于2040吨,则:
240x+200(10-x)≥2040
x≥1
所以x取1或2
若x=1,则需资金1×12+9×10=102万
若x=2,则需资金2×12+8×10=104万
因此为了节约资金,应选择方案二,即A型设备1台,B型设备9台。
【解析】
(1)因为购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元,所以有![]() ,解之即可;
,解之即可;
(2)可设购买污水处理设备A型设备x台,B型设备(10-x)台,则有12x+10(10-x)≤105,解之确定x的值,即可确定方案;
(3)因为每月要求处理洋澜湖的污水量不低于2040吨,所以有240x+180(10-x)≥2040,解之即可由x的值确定方案,然后进行比较,作出选择.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距_____千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时.
(3)B出发后_____小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,点
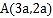 在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,
在第一象限,过点A向x轴作垂线,垂足为点B,连接OA, ,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN.
,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN. 求a的值;
求a的值; 当
当 时,
时, 请探究
请探究 ,
, ,
, 之间的数量关系,并说明理由;
之间的数量关系,并说明理由; 试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由.
试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由. 当
当 时,请求出t的值.
时,请求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
类型价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
(1)请利用二元一次方程组求这两种服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度.
图1为点P在⊙O外的情形示意图.
(1)若点B(1,0),C(1,1),D(0, ),则SB=;SC=;SD=;
),则SB=;SC=;SD=;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR , 直接写出满足条件的线段PQ长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为<x>,即当n为非负整数时,若
 ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:①<1.493>=1;
②<2x>=2<x>;
③若
 ,则实数x的取值范围是
,则实数x的取值范围是 ;
;④当x≥0,m为非负整数时,有
 ;
;⑤
 。
。其中,正确的结论有 (填写所有正确的序号)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程(组)
(1)5x﹣2=3x+8;(2)
 ;(3)
;(3) ;(4)
;(4) .
.
相关试题

