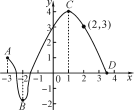
【题目】已知两个变量x,y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出y的变化范围;
(2)求当x=0,-3时,y的对应值;
(3)求当y=0,3时,对应的x的值;
(4)当x为何值时,y的值最大?
(5)当x在什么范围内时,y的值在不断增加?
参考答案:
【答案】(1)y的变化范围为-2~4;(2)当x=0时,y=3;当x=-3时,y=1.(3)当y=0时,x1=-2.5,x2=-1.5,x3=3.5;当y=3时,x1=0,x2=2.(4)当x=1时,图象有最高点,此时y最大.(5)当x在-2~1时,y的值在不断增加.
【解析】
(1)根据函数图象的最高点和最低点的纵坐标,可得答案;
(2)根据自变量的值与函数值的对应关系,即可得出相应的函数值;
(3)根据函数值,即可得出相应自变量的值;
(4)根据函数图象的最高点对应的自变量的值即可得出答案;
(5)根据函数图象上升部分的横坐标,即可得出自变量的范围.
(1)根据函数图象可得:y的变化范围为-2~4.
(2)当x=0时,y=3;当x=-3时,y=1.
(3)当y=0时,x1=-2.5,x2=-1.5,x3=3.5;
当y=3时,x1=0,x2=2.
(4)当x=1时,图象有最高点,此时y最大.
(5)当x在-2~1时,函数图象上升,y的值在不断增加.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备
 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.A型
B型
价格
 万元
万元 台
台
a
b
处理污水量
 吨
吨 月
月
240
200
 求a,b的值;
求a,b的值; 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案; 在
在 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2+4x﹣
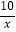 +1=0的正数根的取值范围是( )
+1=0的正数根的取值范围是( )
A.0<x<1
B.1<x<2
C.2<x<3
D.3<x<4 -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如下三个函数图象中,有两个函数图象能近似地刻画如下
 两个情境:
两个情境:
情境
 :小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;
:小芳离开家不久,发现把作业本忘在家里,于是返回家里找到了作业本再去学校;情境
 :小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.
:小芳从家出发,走了一段路程后,为了赶时间,以更快的速度前进.(1)情境
 ,
,  所对应的函数图象分别为 , (填写序号).
所对应的函数图象分别为 , (填写序号).(2)请你为剩下的函数图象写出一个适合的情境.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:

①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
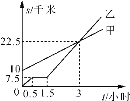
查看答案和解析>>【题目】如图,分别表示甲步行与乙骑自行车(在同一路上)行走的路程s甲,s乙与时间t的关系,观察图象并回答下列问题:
(1)乙出发时,乙与甲相距 千米;
(2)走了一段路程后,乙的自行车发生故障,停下来修车的时间为 小时;
(3)乙从出发起,经过 小时与甲相遇;
(4)乙骑自行车出故障前的速度与修车后的速度一样吗?为什么?
相关试题

