【题目】我们规定:有理数![]() 用数轴上点
用数轴上点![]() 表示,
表示,![]() 叫做点
叫做点![]() 在数轴上的坐标;有理数
在数轴上的坐标;有理数![]() 用数轴上点
用数轴上点![]() 表示,
表示,![]() 叫做点
叫做点![]() 在数轴上的坐标.
在数轴上的坐标.![]() 表示数轴上的两点
表示数轴上的两点![]() ,
,![]() 之间的距离.
之间的距离.
(1)借助数轴,完成下表:
|
|
|
|
3 | 2 | 1 | 1 |
1 | 5 | ______ | ______ |
2 | -3 | ______ | ______ |
-4 | 1 | ______ | ______ |
-5 | -2 | ______ | ______ |
-3 | -6 | ______ | ______ |
(2)观察(1)中的表格内容,猜想![]() ______;(用含
______;(用含![]() ,
,![]() 的式子表示,不用说理)
的式子表示,不用说理)
(3)已知点![]() 在数轴上的坐标是-2,且
在数轴上的坐标是-2,且![]() ,利用(2)中的结论求点
,利用(2)中的结论求点![]() 在数轴上的坐标.
在数轴上的坐标.
参考答案:
【答案】(1)-4,4;5,5;-5,5;-3,3;3,3;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据![]() 表示数轴上的两点A,B之间的距离,即可得到
表示数轴上的两点A,B之间的距离,即可得到![]() 的值;
的值;
(2)根据表格内容,即可猜想![]() ;
;
(3)根据方程![]() ,即可得到
,即可得到![]() 或
或![]() ,进而得出xB=-10或xB=6.
,进而得出xB=-10或xB=6.
(1)![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
故答案为:-4,4;5,5;-5,5;-3,3;3,3;
(2)![]() ;
;
故答案为:![]() ;
;
(3)由题可得,![]() ,
,
∴![]() ,或
,或![]() ,
,
解得![]() 或
或![]() .
.
-
科目: 来源: 题型:
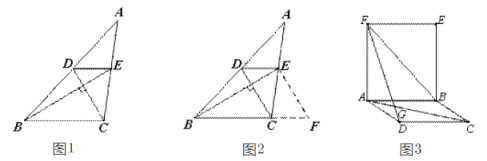
查看答案和解析>>【题目】阅读下面的材料:小锤遇到一个问题:如图①,在△ABC中,DE//BC分别交AB于点D,交AC于点E,已知CD
 BE,CD=2,BE=3,求BC+DE的值.
BE,CD=2,BE=3,求BC+DE的值.小锤发现,过点E作EF
 DC,交BC的延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决.
DC,交BC的延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决.(1)请按照上述思路完成小锤遇到的问题;
(2)参考小锤思考问题的方法,解决下面的问题:如图②,四边形ABCD是平行四边形,四边形ABEF是矩形,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】1883年,德国数学家格奥尔格·康托尔引入位于一条线段上的一些点的集合,它的做法如下:
取一条长度为1的线段,将它三等分,去掉中间一段,余下两条线段,达到第1阶段;将剩下的两条线段再分别三等分,各去掉中间一段,余下四条线段,达到第2阶段;再将剩四条线段,分别三等分,分别去掉中间一段,余下八条线段,达到第3阶段:…;这样的操作一直继续下去,在不断分割舍弃过程中,所形成的线段数目越来越多,把这种分形,称作康托尔点集,如图是康托尔点集的最初几个阶段,当达到第5个阶段时,余下的线段的长度之和为________;当达到第
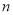 个阶段时(
个阶段时(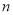 为正整数),余下的线段的长度之和为________.
为正整数),余下的线段的长度之和为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
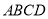 内部有若干个点,用这些点以及正方形
内部有若干个点,用这些点以及正方形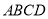 的顶点
的顶点 、
、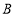 、
、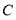 、
、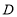 把原正方形分割成一些三角形(互相不重叠)
把原正方形分割成一些三角形(互相不重叠)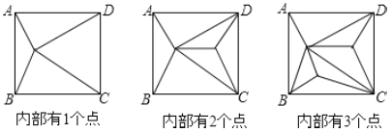
(1)填写下表:
正方形
 内点的个数
内点的个数1
2
3
4
…
分割成的三角形的个数
4
6
______
______
…
______
(2)如果原正方形内有101个点,此时原正方形被分割成多少个三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
-
科目: 来源: 题型:
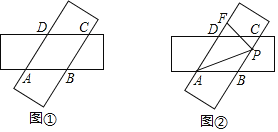
查看答案和解析>>【题目】两张宽度均为4的矩形纸片按如图所示方式放置:
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,点P在BC上,PF
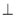 AD于点F,若
AD于点F,若 =16
=16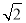 , PC=1.
, PC=1.①求∠BAD的度数;②求DF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD相交于点O,
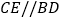 ,
,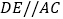 .若
.若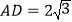 ,
, ,则四边形OCED的面积为___.
,则四边形OCED的面积为___.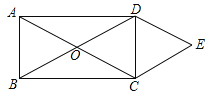
相关试题

