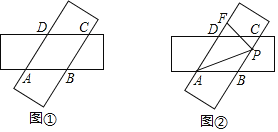
【题目】两张宽度均为4的矩形纸片按如图所示方式放置:
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,点P在BC上,PF![]() AD于点F,若
AD于点F,若![]() =16
=16![]() , PC=1.
, PC=1.
①求∠BAD的度数;②求DF的长.
参考答案:
【答案】(1)见解析;(2)45°;DF=3.
【解析】
(1)过点D作DE⊥AB于E,作DQ⊥BC于Q,构造全等三角形,得出AD=CD,再根据AB∥CD,AD∥BC,得到四边形ABCD是平行四边形,进而得出四边形ABCD是菱形;
(2)①先根据菱形的面积求得菱形的边长,再根据sin∠DAE的值,求得∠BAD的度数;②根据CP=1,以及∠PCG=∠BAD=45°,求得PG=1,再根据∠CDF=45°=∠DGF,即可得到DF=FG=1.
(1)如图1,过点D作DE⊥AB于E,作DQ⊥BC于Q,则∠AED=∠CQD=90°,
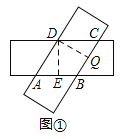
∵矩形纸片宽度均为4,
∴DE=DQ,
又∵∠CDE=∠ADQ=90°,
∴∠ADE=∠CDQ,
在△ADE和△CDQ中,
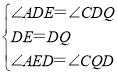 ,
,
∴△ADE≌△CDQ(ASA),
∴AD=CD,
又∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴四边形ABCD是菱形;
(2)①如图1,∵S四边形ABCD=16![]() ,
,
∴AB×DE=16![]() ,即AB×4=16
,即AB×4=16![]() ,
,
∴AB=4![]() =AD,
=AD,
∴sin∠DAE=![]() ,
,
∴∠BAD=45°;
②如图2,
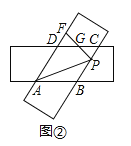
∵PF⊥AD,AD∥BC,
∴PF⊥BC,
又∵∠PCG=∠BAD=45°,
∵PC=1
∴PG=1,
∵PF=4
∴FG=PF-PG=4-1=3,
又∵∠CDF=45°=∠DGF,
∴DF=FG=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
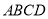 内部有若干个点,用这些点以及正方形
内部有若干个点,用这些点以及正方形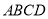 的顶点
的顶点 、
、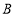 、
、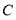 、
、 把原正方形分割成一些三角形(互相不重叠)
把原正方形分割成一些三角形(互相不重叠)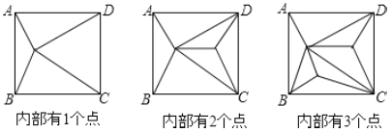
(1)填写下表:
正方形
 内点的个数
内点的个数1
2
3
4
…
分割成的三角形的个数
4
6
______
______
…
______
(2)如果原正方形内有101个点,此时原正方形被分割成多少个三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:有理数
 用数轴上点
用数轴上点 表示,
表示, 叫做点
叫做点 在数轴上的坐标;有理数
在数轴上的坐标;有理数 用数轴上点
用数轴上点 表示,
表示, 叫做点
叫做点 在数轴上的坐标.
在数轴上的坐标. 表示数轴上的两点
表示数轴上的两点 ,
, 之间的距离.
之间的距离.(1)借助数轴,完成下表:




3
2
1
1
1
5
______
______
2
-3
______
______
-4
1
______
______
-5
-2
______
______
-3
-6
______
______
(2)观察(1)中的表格内容,猜想
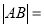 ______;(用含
______;(用含 ,
, 的式子表示,不用说理)
的式子表示,不用说理)(3)已知点
 在数轴上的坐标是-2,且
在数轴上的坐标是-2,且 ,利用(2)中的结论求点
,利用(2)中的结论求点 在数轴上的坐标.
在数轴上的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )

A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC与BD相交于点O,
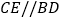 ,
,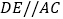 .若
.若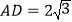 ,
, ,则四边形OCED的面积为___.
,则四边形OCED的面积为___.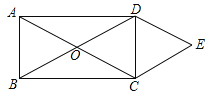
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
(1)求抛物线的解析式;
(2)点D在y轴上,且∠BDO=∠BAC,求点D的坐标;
(3)点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列代数式书写规范的是( )
A. a÷3B. a8C. 5aD.

相关试题

