【题目】阅读下面的情景对话,然后解答问题: 
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
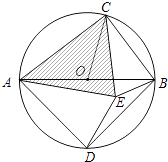
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆 ![]() 的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
参考答案:
【答案】
(1)解:设等边三角形的一边为a,则a2+a2=2a2,
∴符合奇异三角形”的定义.
∴是真命题
(2)解:∵∠C=90°,
则a2+b2=c2①,
∵Rt△ABC是奇异三角形,且b>a,
∴a2+c2=2b2②,
由①②得:b= ![]() a,c=
a,c= ![]() a,
a,
∴a:b:c=1: ![]() :
: ![]()
(3)解:∵①AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2,
∵点D是半圆 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴AD=BD,
∴AB2=AD2+BD2=2AD2,
∴AC2+CB2=2AD2,
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2,
∴△ACE是奇异三角形;
②由①可得△ACE是奇异三角形,
∴AC2+CE2=2AE2,
当△ACE是直角三角形时,
由(2)得:AC:AE:CE=1: ![]() :
: ![]() 或AC:AE:CE=
或AC:AE:CE= ![]() :
: ![]() :1,
:1,
当AC:AE:CE=1: ![]() :
: ![]() 时,AC:CE=1:
时,AC:CE=1: ![]() ,即AC:CB=1:
,即AC:CB=1: ![]() ,
,
∵∠ACB=90°,
∴∠ABC=30°,
∴∠AOC=2∠ABC=60°;
当AC:AE:CE= ![]() :
: ![]() :1时,AC:CE=
:1时,AC:CE= ![]() :1,即AC:CB=
:1,即AC:CB= ![]() :1,
:1,
∵∠ACB=90°,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°.
∴∠AOC的度数为60°或120°.
【解析】(1)根据“奇异三角形”的定义与等边三角形的性质,求证即可;(2)根据勾股定理与奇异三角形的性质,可得a2+b2=c2与a2+c2=2b2 , 用a表示出b与c,即可求得答案;(3)①AB是⊙O的直径,即可求得∠ACB=∠ADB=90°,然后利用勾股定理与圆的性质即可证得;②利用(2)中的结论,分别从AC:AE:CE=1: ![]() :
: ![]() 与AC:AE:CE=
与AC:AE:CE= ![]() :
: ![]() :1去分析,即可求得结果.
:1去分析,即可求得结果.
【考点精析】掌握等边三角形的性质和勾股定理的概念是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C、D四个车站的位置如图所示,A、B两站之间的距离AB=a﹣b,B、C两站之间的距离BC=2a﹣b,B、D两站之间的距离BD=
 a﹣2b﹣1.求:
a﹣2b﹣1.求:(1)A、C两站之间的距离AC;
(2)若A、C两站之间的距离AC=180km,求C、D两站之间的距离CD.
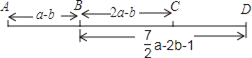
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)先化简
 ,然后从-2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.
,然后从-2≤x≤2的范围内选取一个合适的整数作为x的值代入求值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系xOy中,点A的坐标为(﹣2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
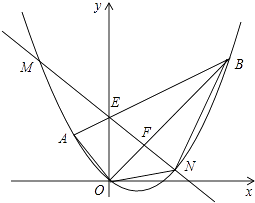
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当点F在线段OB上运动时,求△BON面积的最大值,并求出此时点N的坐标;
(4)连接AN,当△BON面积最大时,在坐标平面内求使得△BOP与△OAN相似(点B、O、P分别与点O、A、N对应)的点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义新运算“△”,对于任意有理数a,b,都有a△b=a2-ab+b,例如:3△5=32-3×5+5=-1,请根据上述知识解决问题:
(1)化简:(x-1)△(2+x);
(2)若(1)中的代数式的值大于6而小于9,求x的取值范围.
相关试题

