搜索
【题目】A、B、C、D四个车站的位置如图所示，A、B两站之间的距离AB＝a﹣b，B、C两站之间的距离BC＝2a﹣b，B、D两站之间的距离BD＝
a﹣2b﹣1．求：
（1）A、C两站之间的距离AC；
（2）若A、C两站之间的距离AC＝180km，求C、D两站之间的距离CD．
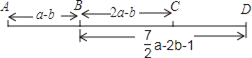
参考答案：
【答案】（1）3a﹣2b；（2）89km．
【解析】
（1）根据两点间的距离列出代数式即可；
（2）根据两点间的距离列出CD的代数式进行解答即可．
（1）A、C两站之间的距离AC＝a﹣b+2a﹣b＝3a﹣2b；
（2）CD＝（
a﹣2b﹣1）﹣（2a﹣b）＝
a﹣b﹣1，
∵3a﹣2b＝180km，
∴a﹣b＝90km，
∴CD＝90﹣1＝89（km）．
答：C、D两站之间的距离CD是89km．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某汽车行驶时油箱中余油量Q（L）与行驶时间t（h）的关系如表：
行驶时间t/h
余油量Q/L
1
42
2
34
3
26
4
18
5
10
（1）汽车行驶之前油箱中有汽油多少升？
（2）用行驶时间t的代数式表示余油量Q（直接写出答案）；
（3）当t＝
时，求余油量Q的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列等式：（1）13＝
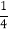×12×22；（2）13+23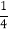＝×22×32；（3）13+23+33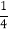＝×32×42；（4）13+23+33+43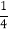＝×42×52；
根据上述等式的规律，解答下列问题：
（1）写出第5个等式：_____；
（2）写出第n个等式（用含有n的代数式表示）；
（3）设s是正整数且s≥2，应用你发现的规律，化简：
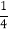×s2×（s+1）2﹣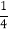×（s﹣1）2×s2． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过点A作AG∥DB交CB的延长线于点G．
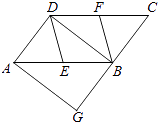
（1）求证：DE∥BF；
（2）若∠G=90°，求证：四边形DEBF是菱形． -
科目： 来源： 题型：
查看答案和解析>>【题目】（8分）先化简
，然后从－2≤x≤2的范围内选取一个合适的整数作为x的值代入求值. -
科目： 来源： 题型：
查看答案和解析>>【题目】我市某林场计划购买甲、乙两种树苗共800株，甲种树苗每株24元，乙种树苗每株30元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．
（1）若购买这两种树苗共用去21000元，则甲、乙两种树苗各购买多少株？
（2）若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？
（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面的情景对话，然后解答问题：
（1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？
（2）在Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇异三角形，求a：b：c；
（3）如图，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆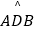
的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE=AD，CB=CE． ①求证：△ACE是奇异三角形；
②当△ACE是直角三角形时，求∠AOC的度数．
相关试题
