【题目】如图,已知AD、AE分别是Rt△ABC的高和中线,AB=9cm,AC=12cm,BC=15cm,试求:
(1)AD的长度;
(2)△ACE和△ABE的周长的差.

参考答案:
【答案】(1)AD的长度为![]() cm;(2)△ACE和△ABE的周长的差是3cm.
cm;(2)△ACE和△ABE的周长的差是3cm.
【解析】
(1)利用直角三角形的面积法来求线段AD的长度;
(2)由于AE是中线,那么BE=CE,再表示△ACE的周长和△ABE的周长,化简可得△ACE的周长﹣△ABE的周长=AC﹣AB即可.
解:(1)∵∠BAC=90°,AD是边BC上的高,
∴S△ACB=![]() ABAC=
ABAC=![]() BCAD,
BCAD,
∵AB=9cm,AC=12cm,BC=15cm,
∴AD=![]() =
=![]() =
=![]() (cm),
(cm),
即AD的长度为![]() cm;
cm;
(2)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长﹣△ABE的周长=AC+AE+CE﹣(AB+BE+AE)=AC﹣AB=12﹣9=3(cm),
即△ACE和△ABE的周长的差是3cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是以AB为直径的⊙M的内接四边形,点A,B在x轴上,△MBC是边长为2的等边三角形,过点M作直线l与x轴垂直,交⊙M于点E,垂足为点M,且点D平分
 .
.
(1)求过A,B,E三点的抛物线的解析式;
(2)求证:四边形AMCD是菱形;
(3)请问在抛物线上是否存在一点P,使得△ABP的面积等于定值5?若存在,请求出所有的点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
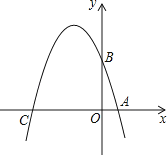
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)求证:AE=EF.
(2)(探究1)变特殊为一般:若题中“点E是边BC的中点”变为“点E是BC边上任意一点”,则上述结论是否仍然成立?(填“是”或“否”).
(3)(探究2)在探究1的前提下,若题中结论“AE=EF”与条件“CF是正方形外角的平分线”互换,则命题是否还成立?请给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有
 、
、 两地,甲乙两人同时出发,甲骑自行车从
两地,甲乙两人同时出发,甲骑自行车从 地到
地到 地,乙骑自行车从
地,乙骑自行车从 地到
地到 地,到达
地,到达 地后立即按原路返回
地后立即按原路返回 地.如图是甲、乙两人离
地.如图是甲、乙两人离 地的距离
地的距离 与行驶时间
与行驶时间 之间的函数图象,下列说法中①
之间的函数图象,下列说法中① 、
、 两地相距30千米;②甲的速度为15千米/时;③点
两地相距30千米;②甲的速度为15千米/时;③点 的坐标为(
的坐标为( ,20);④当甲、乙两人相距10千米时,他们的行驶时间是
,20);④当甲、乙两人相距10千米时,他们的行驶时间是 小时或
小时或 小时. 正确的个数为( )
小时. 正确的个数为( )
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2 , 点A,B的对应点分别为点D,E.

(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,∠ABC=135°,CD=6,AB=2,则四边形ABCD的面积为___________

相关试题

