Question

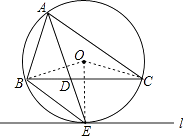
【题目】已知：如图，点A，B，C三点在⊙O上，AE平分∠BAC，交⊙O于点E，交BC于点D，过点E作直线l∥BC，连结BE．
（1）求证：直线l是⊙O的切线；
（2）如果DE=a，AE=b，写出求BE的长的思路．

Answer 1

【答案】
（1）解：如图，连接OE、OB、OC，

∵AE平分∠BAC，

∴∠BAE=∠CAE，

∴ ，

∴∠BOE=∠COE，

∵OB=OC，

∴OE⊥BC，

∵l∥BC，

∴OE⊥l，

∴直线l是⊙O的切线；

（2）∵∠BAE=∠CAE，∠CAE=∠CBE，

∴∠BAE=∠DBE，

又∵∠AEB=∠BED，

∴△ABE∽△BDE，

∴ = ，

∴BE2=AEDE=ab．

【解析】（1）作辅助线，连接半径，由角平分线得：∠BAE=∠CAE，圆周角相等，则弧相等，再由垂径定理证明OE⊥BC，所以OE⊥l，直线l与⊙O相切；（2）根据∠BAE=∠CAE、∠CAE=∠CBE结合公共角证△ABE∽△BDE可得 = ，从而得出答案．