【题目】如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数y= 的图象交于A、B两点，与x轴交于点C；点A在第一象限，点B的坐标为（﹣6，n）；E为x轴正半轴上一点，且tan∠AOE= ．
（1）求点A的坐标；
（2）求一次函数的表达式；
（3）求△AOB的面积．

参考答案：

【答案】
（1）解：过A作AH⊥x轴于点H，

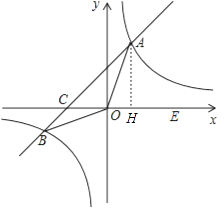
在Rt△AOH中，∵tan∠AOE= = ，

∴设OH=3k，AH=4k，

即A的坐标为（3k，4k），其中k＞0，

∵A在y= 图象上，

∴4k= ，

解得：k=1（负数舍去），

∴A的坐标为（3，4）；


（2）解：∵点B（﹣6，n）在y= 的图象上，

∴代入得：n=﹣2，

即B的坐标为（﹣6，﹣2），

把A、B的坐标代入y=kx+b（k≠0）得： ，

解得：k= ，b=2，

∴一次函数的表达式是y= x+2；


（3）解：在y= x+2中令y=0，则x=﹣3，

即C（﹣3，0），

所以S△AOB=S△AOC+S△BOC= ×|﹣3|×4+ ×|﹣3|×|﹣2|=9，

即△AOB的面积是9．


【解析】（1）过A作AH⊥x轴于点H，根据tan∠AOE= = ，设OH=3k，AH=4k，即A的坐标为（3k，4k），代入反比例函数解析式即可求出A点的坐标；（2）求出B点的坐标，把A、B的坐标代入y=kx+b即可求出k、b的值，即可求出答案；（3）求出OC，根据三角形面积公式求出即可．
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．

关闭