【题目】如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=![]() ,则△ABC的边长为____.
,则△ABC的边长为____.

参考答案:
【答案】3
【解析】
根据等边三角形性质求出AB=BC=AC,∠B=∠C=60°,推出∠BAP=∠DPC,证△BAP∽△CPD,得出![]() ,代入求出即可.
,代入求出即可.
∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠C=60°,
∴∠BAP+∠APB=180°-60°=120°,
∵∠APD=60°,
∴∠APB+∠DPC=180°-60°=120°,
∴∠BAP=∠DPC,
即∠B=∠C,∠BAP=∠DPC,
∴△BAP∽△CPD,
∴![]() ,
,
∵CD=![]() ,CP=BC-BP=x-1,BP=1,
,CP=BC-BP=x-1,BP=1,
即![]() ,
,
解得:AB=3.
故答案为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,

(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为________cm/s时,在某一时刻也能够使△BPE与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD的四条边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在何处?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校
 名学生参加植树活动,要求每人植
名学生参加植树活动,要求每人植 棵,活动结束后随机抽查了
棵,活动结束后随机抽查了 名学生每人的植树量,并分为四种类型,
名学生每人的植树量,并分为四种类型, :
: 棵;
棵; ;
; 棵;
棵; :
: 棵,
棵, :
: 棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
回答下列问题:
(1)写出条形图中存在的错误,并说明理由.
(2)写出这
 名学生每人植树量的众数、中位数.
名学生每人植树量的众数、中位数.(3)在求这
 名学生每人植树量的平均数.
名学生每人植树量的平均数.(4)估计这
 名学生共植树多少棵.
名学生共植树多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①
 ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A. ①②③④ B. ①④ C. ②③④ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1,并写出A1、B1、C1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△A2B2C2,使
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店老板去图书批发市场购买某种图书.第一次用
 元购书若干本,并按该书定价
元购书若干本,并按该书定价 元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了
元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了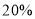 ,他用
,他用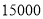 元所购该书数量比第一次多
元所购该书数量比第一次多 本.
本.(1)求两次购书的价格分别是多少?
(2)若第二次购书按定价售出
 本时,出现滞销,于是决定打折出售剩下这批书,那么该商家最低打几折才能保证剩下书的利润率不低于
本时,出现滞销,于是决定打折出售剩下这批书,那么该商家最低打几折才能保证剩下书的利润率不低于 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2, 0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位长度秒匀速运动,物体乙按顺时针方向以2个单位长度秒匀速运动,则两个物体运动后的第2020次相遇点的坐标是( )

A.(2,0)B.(-1,-1)C.( -2,1)D.(-1, 1)
相关试题

