【题目】如图,已知正方形ABCD的边长为10cm,点E在边AB上,且AE=4cm,

(1)如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为________cm/s时,在某一时刻也能够使△BPE与△CQP全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD的四条边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在何处?
参考答案:
【答案】(1)是,4.8;(2)经过![]() 秒点P与点Q第一次在A点相遇.
秒点P与点Q第一次在A点相遇.
【解析】
试题正方形的四边相等,四个角都是直角.(1)①速度相等,运动的时间相等,所以距离相等,根据全等三角形的判定定理可证明.②因为运动时间一样,运动速度不相等,所以BP≠CQ,只有BP=CP时才相等,根据此可求解.
(2)知道速度,知道距离,这实际上是个追及问题,可根据追及问题的等量关系求解.
试题解析:(1)①∵t=1秒,
∴BP=CQ=4×1=4厘米,
∵正方形ABCD中,边长为10厘米
∴PC=BE=6厘米,
又∵正方形ABCD,
∴∠B=∠C,
∴△BPE≌△CQP
②∵VP≠VQ,∴BP≠CQ,
又∵△BPE≌△CQP,∠B=∠C,则BP=PC,
而BP=4t,CP=10-4t,
∴4t=10-4t
∴点P,点Q运动的时间t=![]() 秒,
秒,
∴vq=6÷![]() =4.8厘米/秒.
=4.8厘米/秒.
(2)设经过x秒后点P与点Q第一次相遇,
由题意,得4.8x-4x=30,
解得x=![]() 秒.
秒.
∴点P共运动了![]() ×4=150厘米
×4=150厘米
∴点P、点Q在A点相遇,
∴经过![]() 秒点P与点Q第一次在A点相遇.
秒点P与点Q第一次在A点相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中, 于点
于点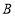 ,
, 于点
于点 ,
, 平分
平分 ,且点
,且点 为
为 的中点,连接
的中点,连接 .
.
(1)求证:
 平分
平分 ;
;(2)求
 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要测量河流
 的长,因为无法测河流附近的点
的长,因为无法测河流附近的点 ,可以在
,可以在 线外任取一点
线外任取一点 ,在
,在 的延长线上任取一点
的延长线上任取一点 ,连结
,连结 和
和 ,并且延长
,并且延长 到点
到点 ,使
,使 ;延长
;延长 到点
到点 ,使
,使 连结
连结 ,并延长
,并延长 到点
到点 ,使点
,使点 ,
, ,
, 在同一直线上.证明:测量出线段
在同一直线上.证明:测量出线段 的长就是河流
的长就是河流 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校
 名学生参加植树活动,要求每人植
名学生参加植树活动,要求每人植 棵,活动结束后随机抽查了
棵,活动结束后随机抽查了 名学生每人的植树量,并分为四种类型,
名学生每人的植树量,并分为四种类型, :
: 棵;
棵; ;
; 棵;
棵; :
: 棵,
棵, :
: 棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
棵。将各类的人绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误。
回答下列问题:
(1)写出条形图中存在的错误,并说明理由.
(2)写出这
 名学生每人植树量的众数、中位数.
名学生每人植树量的众数、中位数.(3)在求这
 名学生每人植树量的平均数.
名学生每人植树量的平均数.(4)估计这
 名学生共植树多少棵.
名学生共植树多少棵. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①
 ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
A. ①②③④ B. ①④ C. ②③④ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=
 ,则△ABC的边长为____.
,则△ABC的边长为____.
相关试题

