【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠ACO=![]() .
.

(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值;
(3)在(2)的条件下,以点E为端点,在直线EP的右侧作一条射线与抛物线交于点N,使得∠NEP为锐角,在线段EB上是否存在点G,使得以E,N,G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为y=x2﹣3x﹣4.(2)当a=1时,PM有最大值,最大值为4.(3)存在,点G的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)先由锐角三角函数的定义求得C的坐标,从而得到点B的坐标,设抛物线的解析式为y=a(x+1)(x﹣4),将点C的坐标代入求解即可;
(2)先求得抛物线的对称轴,从而得到点D(3,﹣4),然后可求得直线AD的解析式y=﹣x﹣1,故∠BAD=45°,接下来证明△PMD为等腰直角三角形,所当PM有最大值时三角形的周长最大,设P(a,a2﹣3a﹣4),M(﹣a﹣1),则PM=﹣a2+2a+3,然后利用配方可求得PM的最大值,最后根据△MPH的周长=(1+![]() )PM求解即可;
)PM求解即可;
(3)当∠EGN=90°时,如果![]() 或
或![]() ,则△AOC∽△EGN,设点G的坐标为(a,0),则N(a,a2﹣3a﹣4),则EG=a﹣1,NG=﹣a2+3a+4,然后根据题意列方程求解即可.
,则△AOC∽△EGN,设点G的坐标为(a,0),则N(a,a2﹣3a﹣4),则EG=a﹣1,NG=﹣a2+3a+4,然后根据题意列方程求解即可.
解:(1)∵点A的坐标为(﹣1,0),
∴OA=1.
又∵tan∠ACO=![]() ,
,
∴OC=4.
∴C(0,﹣4).
∵OC=OB,
∴OB=4
∴B(4,0).
设抛物线的解析式为y=a(x+1)(x﹣4).
∵将x=0,y=﹣4代入得:﹣4a=﹣4,解得a=1,
∴抛物线的解析式为y=x2﹣3x﹣4.
(2)∵抛物线的对称轴为x=﹣![]() =
=![]() ,C(0,﹣4),点D和点C关于抛物线的对称轴对称,
,C(0,﹣4),点D和点C关于抛物线的对称轴对称,
∴D(3,﹣4).
设直线AD的解析式为y=kx+b.
∵将A(﹣1,0)、D(3,﹣4)代入得:![]() ,解得k=﹣1,b=﹣1,
,解得k=﹣1,b=﹣1,
∴直线AD的解析式y=﹣x﹣1.
∵直线AD的一次项系数k=﹣1,
∴∠BAD=45°.
∵PM平行于y轴,
∴∠AEP=90°.
∴∠PMH=∠AME=45°.
∴△MPH的周长=PM+MH+PH=PM+![]() MP+
MP+![]() PM=(1+
PM=(1+![]() )PM.
)PM.
设P(a,a2﹣3a﹣4),M(﹣a﹣1),则PM=﹣a﹣1﹣(a2﹣3a﹣4)=﹣a2+2a+3,
∵PM=﹣a2+2a+3=﹣(a﹣1)2+4,
∴当a=1时,PM有最大值,最大值为4.
∴△MPH的周长的最大值=4×(1+![]() )=4+4
)=4+4![]() .
.
(3)如图1所示;当∠EGN=90°.

设点G的坐标为(a,0),则N(a,a2﹣3a﹣4).
∵∠EGN=∠AOC=90°,
∴![]() 时,△AOC∽△EGN.
时,△AOC∽△EGN.
∴![]() =
=![]() ,整理得:a2+a﹣8=0.
,整理得:a2+a﹣8=0.
解得:a=![]() (负值已舍去).
(负值已舍去).
∴点G的坐标为(![]() ,0).
,0).
如图2所示:当∠EGN=90°.

设点G的坐标为(a,0),则N(a,a2﹣3a﹣4).
∵∠EGN=∠AOC=90°,
∴![]() 时,△AOC∽△NGE.
时,△AOC∽△NGE.
∴![]() =4,整理得:4a2﹣11a﹣17=0.
=4,整理得:4a2﹣11a﹣17=0.
解得:a=![]() (负值已舍去).
(负值已舍去).
∴点G的坐标为(![]() ,0).
,0).
∵EN在EP的右面,
∴∠NEG<90°.
如图3所示:当∠ENG′=90°时,

EG′=EG×![]() ×
×![]() =(
=(![]() ﹣1)×
﹣1)×![]() =
=![]() .
.
∴点G′的横坐标=![]() .
.
∵![]() ≈4.03>4,
≈4.03>4,
∴点G′不在EG上.
故此种情况不成立.
综上所述,点G的坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果零上5℃记作+5℃,那么零下7℃可记作_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列与垂直相交的说法:①平面内,垂直于同一条直线的两条直线互相平行;②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;③平面内, 一条直线不可能与两条相交直线都垂直,其中说法错误个数有( )
A. 3个 B. 2个
C. 1个 D. 0个
-
科目: 来源: 题型:
查看答案和解析>>【题目】
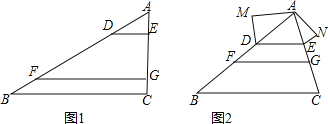
(1)如图①,在△ABC中,点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,若AD=2,AE=1,DF=4,则EG= ,
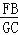 = .
= .(2)如图②,在△ABC中点D、F在AB上,点E,G在AC上,且DE∥FG∥BC,以AD,DF,FB为边构造△ADM(即AM=BF,MD=DF),以AE,EG,GC为边构造△AEN(即AN=GC,NE=EG),求证:∠M=∠N.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在ΔABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。
①求证:OE=OF;
②当点O运动到何处时,四边形AECF是矩形?并请说明理由。
③当点O运动到AC边的中点时,在ΔABC中添加一个什么条件后,四边形AECF是正方形。(只需写出一个条件,不必证明)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:
事件A
必然事件
随机事件
m的值
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于
 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在Rt△ABC中,AC⊥BC,CD⊥AB于D,AG平分∠BAC,交BC于G,交CD于E,EF∥AB交BC于F,求证:CE=BF.

相关试题

