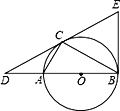
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
参考答案:
【答案】(1)![]() ;(2)直线EB与
;(2)直线EB与![]() 相切,证明见解析.
相切,证明见解析.
【解析】试题分析:(1)根据DA:AB=1:2,得到DA等于圆的半径.连接过切点的半径,构造直角三角形,利用解直角三角形的知识求解;
(2)连接OC.根据(1)中的结论,可以知道直角![]() 有一个角为30°.根据圆周角定理发现
有一个角为30°.根据圆周角定理发现![]() 得到
得到![]() 进一步得到等边
进一步得到等边![]() .则
.则![]() 根据切线的判定即可证明.
根据切线的判定即可证明.
试题解析:(1)如图,连接OC,

∵CD是![]() 的切线,
的切线,
![]()
设![]() 的半径为R,则AB=2R,
的半径为R,则AB=2R,
∵DA:AB=1:2,
∴DA=R,DO=2R.
在Rt△DOC中, ![]()
![]() 即
即![]()
(2)直线EB与![]() 相切,
相切,
证明:连接OC,
由(1)可知![]()
![]()
∵OC=OB,
![]()
∴∠CBD=∠CDB.
∴CD=CB.
∵CD是![]() 的切线,
的切线,
![]()
![]() 又∵CD=CE,
又∵CD=CE,
∴CB=CE.
∴△CBE为等边三角形,
![]()
∴EB是![]() 的切线.
的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,反比例函数y=
 的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, 交
交 于点
于点 ,交
,交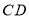 于点
于点 ,
, 平分
平分 ,若
,若 ,求
,求 的度数.请补充完成以下求解过程:
的度数.请补充完成以下求解过程:
解:∵
 (___①___)
(___①___) (_______②___)
(_______②___)

 __________③_______
__________③_______ (_______④_______)
(_______④_______)


∴___________⑤_______(______⑥_______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张长方形纸板按图中虚线裁剪成
 块,其中有
块,其中有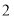 块是边长都为
块是边长都为 厘米的大正方形,
厘米的大正方形,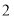 块是边长都为
块是边长都为 厘米的小正方形,
厘米的小正方形, 块是长为
块是长为 厘米,宽为
厘米,宽为 厘米的一模一样的小长方形,且
厘米的一模一样的小长方形,且 ,设图中所有裁剪线(虚线部分)长之和为
,设图中所有裁剪线(虚线部分)长之和为 厘米.
厘米.
(1)
 ______(试用
______(试用 ,
, 的代数式表示);
的代数式表示);(2)若每块小长方形的面积为
 平方厘米,四个正方形的面积和为
平方厘米,四个正方形的面积和为 平方厘米,求
平方厘米,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生能更加了解温州历史,某校组织七年级师生共480人参观温州博物馆.学校向租车公司租赁A、B两种车型接送师生往返,若租用A型车3辆,B型车6辆,则空余15个座位;若租用A型车5辆,B型车4辆,则15人没座位.
(1)求A、B两种车型各有多少个座位;
(2)若A型车日租金为350元,B型车日租金为400元,且租车公司最多能提供7辆B型车,应怎样租车能使座位恰好坐满且租金最少,并求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.

(1)求单摆的长度;
(2)求从点A摆动到点B经过的路径长.
相关试题

