【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
参考答案:
【答案】(1)![]() (0<x<8);(2)能;(3)当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
(0<x<8);(2)能;(3)当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
【解析】
试题分析:(1)由矩形的一边长为x、周长为16得出另一边长为8﹣x,根据矩形的面积公式可得答案;
(2)由设计费为24000元得出矩形面积为12平方米,据此列出方程,解之求得x的值,从而得出答案;
(3)将函数解析式配方成顶点式,可得函数的最值情况.
试题解析:(1)∵矩形的一边为x米,周长为16米,∴另一边长为(8﹣x)米,∴S=x(8﹣x)=![]() ,其中0<x<8,即
,其中0<x<8,即![]() (0<x<8);
(0<x<8);
(2)能,∵设计费能达到24000元,∴当设计费为24000元时,面积为24000÷200=12(平方米),即![]() =12,解得:x=2或x=6,∴设计费能达到24000元.
=12,解得:x=2或x=6,∴设计费能达到24000元.
(3)∵![]() =
=![]() ,∴当x=4时,S最大值=16,∴当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
,∴当x=4时,S最大值=16,∴当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果电影院的6排3号座位用(6,3)表示,那么该影院的7排5号座位可以表示为_.
-
科目: 来源: 题型:
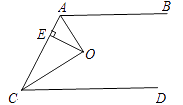
查看答案和解析>>【题目】如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,CO=3,则两平行线间AB、CD的距离等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判定直角三角形全等的方法,不正确的是( )
A. 斜边和一锐角对应相等
B. 两锐角对应相等
C. 两条直角边对应相等
D. 斜边和一条直角边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线
 与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.(1)求该抛物线的解析式;
(2)直线y=﹣x+n与该抛物线在第四象限内交于点D,与线段BC交于点E,与x轴交于点F,且BE=4EC.
①求n的值;
②连接AC,CD,线段AC与线段DF交于点G,△AGF与△CGD是否全等?请说明理由;
(3)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧),点 M关于y轴的对称点为点M',点H的坐标为(1,0).若四边形OM'NH的面积为
 .求点H到OM'的距离d的值.
.求点H到OM'的距离d的值.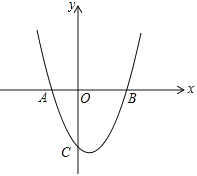
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,∠1=∠2,∠B=∠C,则BD=CE.请说明理由:

解:∵∠1=∠2
∴∠1+∠BAC=∠2+ .
即=∠DAB.
在△ABD和△ACE中,
∠B=(已知)
∵AB= (已知)
∠EAC=(已证)
∴△ABD≌△ACE()
∴BD=CE( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.
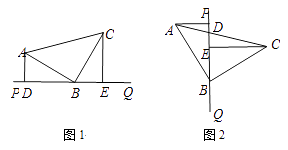
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.
(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD,DE,CE有怎样的等量关系?说明理由.
相关试题

