【题目】如图1,点E是等边△ABC的边BC上一点,以AE为边作等边△AEF,EF交AC于D.
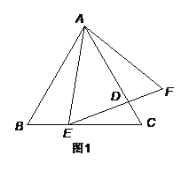
(1)连接CF,求证:![]()
(2)如图2,作EH AF交AB于点H.
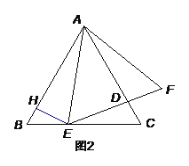
①求证:![]() ;
;
②若EH=2,ED=4,直接写出BE的长为 _________.
参考答案:
【答案】(1)证明见解析(2)见解析(3)![]()
【解析】(1)由等边三角形的性质,根据两角对应相等的两三角形相似,再根据相似三角形的对应边成比例;
(2)①根据相似三角形的对应边成比例证明即可;
②可证EA=EH+ED=6, 作AM⊥BC于M,然后根据勾股定理求解.
(1)∵△ABC,△AEF都是等边三角形,∴AB=AC,∠AEF=∠C=600,
又∵∠EAD=∠CAE,,∴![]() ∽
∽![]() , ∴
, ∴![]()
∵AB=AC ∴![]()
(2)①∵EH∥AF , ∴∠AEH=∠EAF=60°=∠B
方法1:∵![]() ∽
∽![]() ∴
∴![]()
又![]() ∽
∽![]() , ∴
, ∴![]()
∴![]() ,即
,即![]()
②可证EA=EH+ED=6, 作AM⊥BC于M,可设BE=2x,EC=4x,则EM=x, ![]() ,
,
由勾股定理得![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
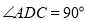 ,
,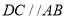 ,
,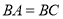 ,
,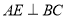 ,垂足为点
,垂足为点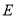 ,点
,点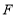 为
为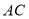 的中点.
的中点.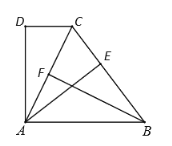
(1) 求证:
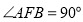 ;
; (2) 求证:
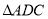 ≌
≌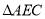 ;
; (3) 联结
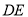 ,试判断
,试判断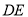 与
与 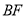 的位置关系,并证明.
的位置关系,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
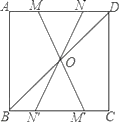
A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)写出点A,B,C的坐标并画出三角形ABC;
(2)若将三角形ABC平移后得到三角形A1B1C1,平移后点C的对应点C1的坐标为(2,1),请画出三角形A1B1C1,并写出A1,B1的坐标.

-
科目: 来源: 题型:
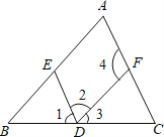
查看答案和解析>>【题目】请结合图形完成下列推理过程:
(1)∵∠2+∠4=180°,
∴DE∥AC (______).
(2)∵∠1=∠C,
∴DE∥______(______).
(3)∵AB∥DF,
∴∠2=∠______(______).
(4)∵______∥______,
∴∠B=∠3 (______).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列三个结论: ①∠AOB=90°+
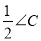 ;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab,其中正确的是( )
;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab,其中正确的是( )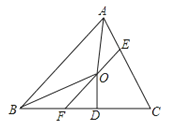
A. ①②③B. ①③C. ①②D. ①
-
科目: 来源: 题型:
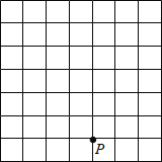
查看答案和解析>>【题目】如图,网格中每个小正方形的边长均为1个单位长度,点P的坐标为(2,-2),请解答下列问题:
(1)将平面直角坐标系补充完整,并描出下列各点:A(-1,0),B(3,-1),C(4,3);
(2)顺次连接A,B,C,组成三角形ABC,求三角形ABC的面积.
相关试题

