【题目】请结合图形完成下列推理过程:
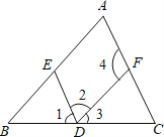
(1)∵∠2+∠4=180°,
∴DE∥AC (______).
(2)∵∠1=∠C,
∴DE∥______(______).
(3)∵AB∥DF,
∴∠2=∠______(______).
(4)∵______∥______,
∴∠B=∠3 (______).
参考答案:
【答案】见解析
【解析】
(1)运用了同旁内角互补,两直线平行;
(2)运用了同位角相等,两直线平行;
(3)运用了两直线平行,内错角相等;
(4)运用了两直线平行,同位角相等.
解:(1)∵∠2+∠4=180°,
∴DE∥AC (同旁内角互补,两直线平行 ).
(2)∵∠1=∠C,
∴DE∥AC(同位角相等,两直线平行).
(3)∵AB∥DF,
∴∠2=∠BED(两直线平行,内错角相等).
(4)∵AB∥DF,
∴∠B=∠3 (两直线平行,同位角相等).
故答案为:同旁内角互补,两直线平行;AC,同位角相等,两直线平行;
BED,两直线平行,内错角相等;AB,DF,两直线平行,同位角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )
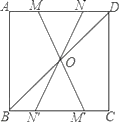
A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)写出点A,B,C的坐标并画出三角形ABC;
(2)若将三角形ABC平移后得到三角形A1B1C1,平移后点C的对应点C1的坐标为(2,1),请画出三角形A1B1C1,并写出A1,B1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点E是等边△ABC的边BC上一点,以AE为边作等边△AEF,EF交AC于D.
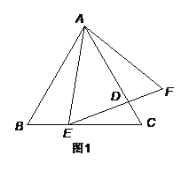
(1)连接CF,求证:
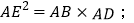
(2)如图2,作EH AF交AB于点H.
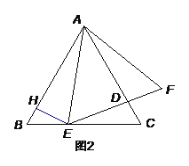
①求证:
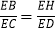 ;
;②若EH=2,ED=4,直接写出BE的长为 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列三个结论: ①∠AOB=90°+
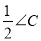 ;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab,其中正确的是( )
;②当∠C=90°时,E,F分别是AC,BC的中点;③若OD=a,CE+CF=2b,则S△CEF=ab,其中正确的是( )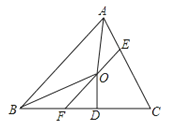
A. ①②③B. ①③C. ①②D. ①
-
科目: 来源: 题型:
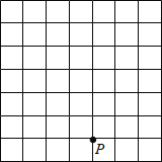
查看答案和解析>>【题目】如图,网格中每个小正方形的边长均为1个单位长度,点P的坐标为(2,-2),请解答下列问题:
(1)将平面直角坐标系补充完整,并描出下列各点:A(-1,0),B(3,-1),C(4,3);
(2)顺次连接A,B,C,组成三角形ABC,求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
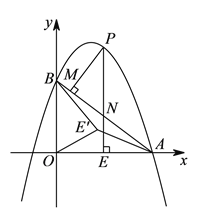
 ,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
,抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0),与y轴交于点B,在X轴上有一动点E(m,0)(0<m<8),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(
 )分别求出直线AB和抛物线的函数表达式;
)分别求出直线AB和抛物线的函数表达式;(
 )设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;
)设△PMN的面积为S1,△AEN的面积为S2,若S1:S2=36:25,求m的值;(
 )如图2,在(
)如图2,在( )条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.
)条件下,将线段OE绕点O逆时针旋转得到OE',旋转角为α(0°<α<90°),连接E'A、E'B.①在x轴上找一点Q,使△OQE'∽△OE'A,并求出Q点的坐标;
②求BE'+
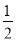 AE'的最小值.
AE'的最小值.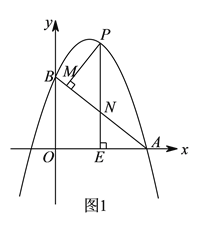
相关试题

