【题目】如图:![]() 中,
中,![]() .
.

![]() 求作
求作![]() 边上的垂直平分线
边上的垂直平分线![]() ,使得
,使得![]() 交
交![]() 于
于![]() ;将线段
;将线段![]() 沿着
沿着![]() 的方向平移到线段
的方向平移到线段![]() (其中点
(其中点![]() 平移到点
平移到点![]() ,画出平移后的线段
,画出平移后的线段![]() ;(要求用尺规作图,不写作法,保留作图痕迹.)
;(要求用尺规作图,不写作法,保留作图痕迹.)
![]() 连接
连接![]() 、
、![]() ,试判断四边形
,试判断四边形![]() 是矩形吗?说明理由.
是矩形吗?说明理由.
参考答案:
【答案】 (1)作图见解析;(2)证明见解析.
【解析】
(1)以B,C为圆心,大于![]() BC长为半径化弧,两弧交于一点,过A与这一点作直线MN,MN为所求的BC的垂直平分线;以D为圆心,AB长为半径化弧,再以A为圆心,BD长为半径化弧,两弧交于一点E,连接DE,线段DE为平移后的线段;
BC长为半径化弧,两弧交于一点,过A与这一点作直线MN,MN为所求的BC的垂直平分线;以D为圆心,AB长为半径化弧,再以A为圆心,BD长为半径化弧,两弧交于一点E,连接DE,线段DE为平移后的线段;
(2)首先证明四边形ADCE为平行四边形,再证明对角线AC=DE,可证出要求的结论.
![]() 如图,
如图,![]() 为所求的
为所求的![]() 的垂直平分线;
的垂直平分线;
线段![]() 为平移后的线段;
为平移后的线段;
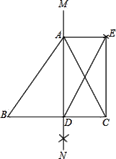
![]() 四边形
四边形![]() 为矩形,理由如下:
为矩形,理由如下:
由平移的特征得:![]() ,
,![]() 且
且![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() 且
且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∵![]() ,
,
∴![]() ,
,
∴平行四边形![]() 为矩形.
为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
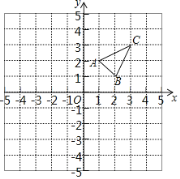
(1)作出与△ABC关于x轴对称的△A1B1C1;
(2)将△ABC向左平移4个单位长度,画出平移后的△A2B2C2;
(3)若在如图的网格中存在格点P,使点P的横、纵坐标之和等于点C的横、纵坐标之和,请写出所有满足条件的格点P的坐标(C除外).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O
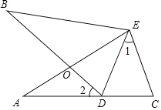
(1)求证:△AEC≌△BED;
(2)若∠1=38°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是正方形,点
是正方形,点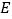 是
是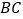 的中点,
的中点, ,
, 交正方形外角的平分线
交正方形外角的平分线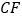 于
于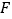 ,连接
,连接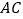 、
、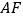 、
、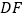 ,求证:
,求证: ;
;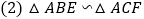 ;
; 是等腰直角三角形.
是等腰直角三角形.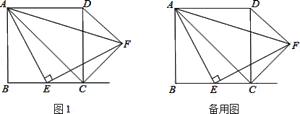
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)

-
科目: 来源: 题型:
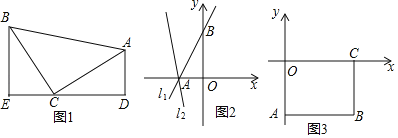
查看答案和解析>>【题目】(模型建立)(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E,求证:△BEC≌△CDA.
(模型应用)(2)①已知直线l1:y=
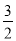 x+3与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+3与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,﹣6),点A、C分别在坐标轴上,点P是线段BC上的动点,若△APD是以点D为直角顶点的等腰直角三角形,当点D在直线y=﹣2x+5上时,直接写出点D的坐标,并写出整个运动过程中点D的纵坐标n的取值范围.
相关试题

