【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于
于![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,求证:
,求证:
![]() ;
;
![]() ;
;
![]() 是等腰直角三角形.
是等腰直角三角形.
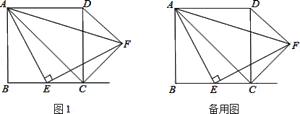
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)取AB中点M,连接ME,利用正方形的性质和等腰直角三角形的性质,证明△AME△ECF,即可得出结论;
(2)利用(1)图,△AEF是等腰直角三角形,继而得到∠2=∠4、∠ACF=∠B,即可证得结论;
(3)过F分别作FN⊥BC的延长线于N,证得△FNE△EBA,得出△FCN是等腰直角三角形,易证四边形FNCP为矩形(正方形),求得∠FDC=∠DCF,得出结论.
![]() 如图
如图![]() ,
,

取![]() 中点
中点![]() ,连接
,连接![]() ,
,
则![]() 正方形边长,
正方形边长,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() 是正方形外角的平分线,
是正方形外角的平分线,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ;
;
![]() 如图
如图![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,即
,即![]() ,
,
∵![]() 为正方形
为正方形![]() 的对角线,
的对角线,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 如图
如图![]() ,
,

设正方形![]() 边长为
边长为![]() ,则
,则![]() ,
,![]() ,
,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
过![]() 作
作![]() 的延长线于
的延长线于![]() ,
,
则![]() ,
,
又由![]() 知,
知,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形(正方形),
为矩形(正方形),
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形.
是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
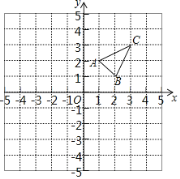
(1)作出与△ABC关于x轴对称的△A1B1C1;
(2)将△ABC向左平移4个单位长度,画出平移后的△A2B2C2;
(3)若在如图的网格中存在格点P,使点P的横、纵坐标之和等于点C的横、纵坐标之和,请写出所有满足条件的格点P的坐标(C除外).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O
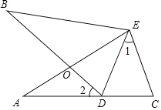
(1)求证:△AEC≌△BED;
(2)若∠1=38°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:
 中,
中, .
.
 求作
求作 边上的垂直平分线
边上的垂直平分线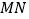 ,使得
,使得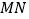 交
交 于
于 ;将线段
;将线段 沿着
沿着 的方向平移到线段
的方向平移到线段 (其中点
(其中点 平移到点
平移到点 ,画出平移后的线段
,画出平移后的线段 ;(要求用尺规作图,不写作法,保留作图痕迹.)
;(要求用尺规作图,不写作法,保留作图痕迹.) 连接
连接 、
、 ,试判断四边形
,试判断四边形 是矩形吗?说明理由.
是矩形吗?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(模型建立)(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E,求证:△BEC≌△CDA.
(模型应用)(2)①已知直线l1:y=
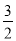 x+3与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
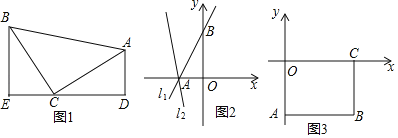
x+3与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,﹣6),点A、C分别在坐标轴上,点P是线段BC上的动点,若△APD是以点D为直角顶点的等腰直角三角形,当点D在直线y=﹣2x+5上时,直接写出点D的坐标,并写出整个运动过程中点D的纵坐标n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
相关试题

