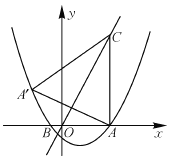
【题目】抛物线y=![]() x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() .(2)点A/的坐标为(﹣3,4).点A/在该抛物线上.(3)点P运动到
.(2)点A/的坐标为(﹣3,4).点A/在该抛物线上.(3)点P运动到![]() 时,四边形PACM是平行四边形.
时,四边形PACM是平行四边形.
【解析】试题分析:(1)将点A、B的坐标代入抛物线的解析式,得到关于b、c的二元一次方程组,从而可解得b、c的值;
(2)过点B′作B′E⊥x轴于E,BB′与OC交于点F.由平行于y轴的直线上各点横坐标相同可知点C的横坐标为2,将x=2代入直线y=﹣2x的解析式可求得点C的坐标∵点B和B′关于直线y=﹣2x对称,在Rt△ABC中,由勾股定理可求得OC=5![]() ,然后利用面积法可求得BF=2
,然后利用面积法可求得BF=2![]() .由轴对称图形的性质可知B′F=FB=4
.由轴对称图形的性质可知B′F=FB=4![]() .由同角的余角相等可证明∠B′BE=∠BCF,从而可证明Rt△B′EB∽Rt△OBC,由相似三角形的性质可求得B′E=4,BE=8,故此可求得点B′的坐标为(﹣3,﹣4),然后可判断出点B′在抛物线上;
.由同角的余角相等可证明∠B′BE=∠BCF,从而可证明Rt△B′EB∽Rt△OBC,由相似三角形的性质可求得B′E=4,BE=8,故此可求得点B′的坐标为(﹣3,﹣4),然后可判断出点B′在抛物线上;
(3)先根据题意画出图形,然后利用待定系数法求得B′C的解析式,设点P的坐标为(x,﹣![]() +x+
+x+![]() ),则点D为(x,﹣
),则点D为(x,﹣![]() ),由平行四边形的判定定理可知当PD=BC时.四边形PBCD是平行四边形,最后根据PD=BC列出关于x的方程即可求得点P的坐标
),由平行四边形的判定定理可知当PD=BC时.四边形PBCD是平行四边形,最后根据PD=BC列出关于x的方程即可求得点P的坐标
解:(1)∵y=![]() x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,
x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,
∴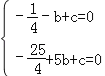 .
.
解得:![]() .
.
∴抛物线的解析式为y=﹣![]() +x+
+x+![]() .
.
(2)如图,过点B′作B′E⊥x轴于E,BB′与OC交于点F.
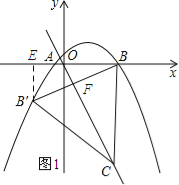
∵BC⊥x轴,
∴点C的横坐标为5.
∵点C在直线y=﹣2x上,
∴C(5,﹣10).
∵点B和B′关于直线y=﹣2x对称,
∴B′F=BF.
在Rt△ABC中,由勾股定理可知:OC=![]() =
=![]() =5
=5![]() .
.
∵S△OBC=![]() OCBF=
OCBF=![]() OBBC,
OBBC,
∴5![]() ×BF=5×10.
×BF=5×10.
∴BF=2![]() .
.
∴BB′=4![]() .
.
∵∠B′BE+∠B′BC=90°,∠BCF+∠B′BC=90°,
∴∠B′BE=∠BCF.
又∵∠B′EB=∠OBC=90°,
∴Rt△B′EB∽Rt△OBC.
∴![]() ,即
,即![]() .
.
∴B′E=4,BE=8.
∴OE=BE﹣OB=3.
∴点B′的坐标为(﹣3,﹣4).
当x=﹣3时,y=﹣![]() ×(﹣3)2+
×(﹣3)2+![]() =﹣4.
=﹣4.
所以,点B′在该抛物线上.
(3)存在.
理由:如图所示:
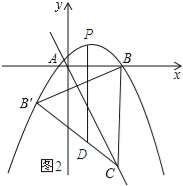
设直线B′C的解析式为y=kx+b,则![]() ,解得:
,解得: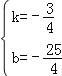
∴直线B′C的解析式为y=![]() .
.
设点P的坐标为(x,﹣![]() +x+
+x+![]() ),则点D为(x,﹣
),则点D为(x,﹣![]() ).
).
∵PD∥BC,
∴要使四边形PBCD是平行四边形,只需PD=BC.又点D在点P的下方,
∴![]() ﹣(﹣
﹣(﹣![]() )=10..
)=10..
解得x1=2,x2=5(不合题意,舍去).
当x=2时,![]() =
=![]() .
.
∴当点P运动到(2,![]() )时,四边形PBCD是平行四边形.
)时,四边形PBCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系
 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形。
(1)你认为图②中阴影部分的正方形的边长等于________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①___________________________________.
方法②___________________________________.
(3)观察图②,试写出
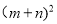 ,
, ,
, 这三个代数式之间的等量关系 .
这三个代数式之间的等量关系 .(4)根据(3)题中的等量关系,解决如下问题:若
 ,
, ,则求
,则求 的值。
的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:

(1)将点B向右移动三个单位长度后到达点D,点D表示的数是 ;
(2)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请你直接写出所有点A移动的距离和方向;
(3)若A、B、C三个点移动后得到三个互不相等的有理数,它们既可以表示为1,
 ,
, 的形式,又可以表示为0,
的形式,又可以表示为0, ,
, 的形式,试求
的形式,试求 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地举行龙舟赛,甲、乙两队在比赛时,路程
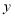 (米)与时间
(米)与时间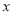 (分钟)的函数图象如图所示,根据函数图象填空和解答问题:
(分钟)的函数图象如图所示,根据函数图象填空和解答问题: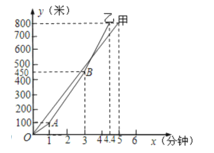
(1)最先到达终点的是_________队,比另一队领先_________分钟到达;
(2)在比赛过程中,甲队的速度始终保持为_________米/分;而乙队在第________分钟后第一次加速,速度变为_________米/分,在第__________分钟后第二次加速;
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由若干个正方体形状的木块堆成的,平放于桌面上。其中,上面正方体的下底面的四个顶点恰是下面相邻正方体的上底面各边的中点,如果最下面的正方体的棱长为1.
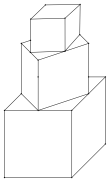
(1)当只有两个正方体放在一起时,这两个正方体露在外面的面积和是 ;
(2)当这些正方体露在外面的面积和超过
 时,那么正方体的个数至少是多少?
时,那么正方体的个数至少是多少?(3)按此规律下去,这些正方体露在外面的面积会不会一直增大?如果会,请说明理由;如果不会,请求出不会超过哪个数值?(提示:所有正方体侧面面积加上所有正方体上面露出的面积之和,就是需求的面积,从简单入手,归纳规律.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象是( )
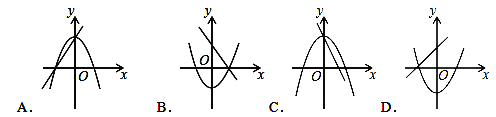
A. A B. B C. C D. D
相关试题

