【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形。
(1)你认为图②中阴影部分的正方形的边长等于________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①___________________________________.
方法②___________________________________.
(3)观察图②,试写出![]() ,
,![]() ,
,![]() 这三个代数式之间的等量关系 .
这三个代数式之间的等量关系 .
(4)根据(3)题中的等量关系,解决如下问题:若![]() ,
,![]() ,则求
,则求![]() 的值。
的值。

参考答案:
【答案】(1)mn;(2)①:(mn)2;②(m+n)24mn;(3)(mn)2=(m+n)24mn;(4)17.
【解析】
平均分成后,每个小长方形的长为m,宽为n.
(1)正方形的边长=小长方形的长-宽;
(2)第一种方法为:大正方形面积-4个小长方形面积,第二种表示方法为:阴影部分为小正方形的面积;
(3)利用(m+n)2-4mn=(m-n)2可求解;
(4)利用(a-b)2=(a+b)2-4ab可求解.
(1)阴影部分的正方形的边长等于mn;
(2)图②中阴影部分的面积,
方法①:(mn)2;方法
②:(m+n)24mn;
(3)三个代数式之间的等量关系:(mn)2=(m+n)24mn;
(4)由(3)可知:(ab)2=(a+b)24ab,
当a+b=5,ab=2时,原式=524×2=17.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
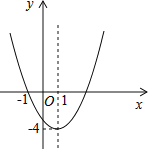
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是﹣4
C.﹣1和3是方程ax2+bx+c=0(a≠0)的两个根
D.当x<1时,y随x的增大而增大
-
科目: 来源: 题型:
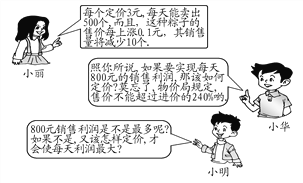
查看答案和解析>>【题目】今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系
 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:

(1)将点B向右移动三个单位长度后到达点D,点D表示的数是 ;
(2)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请你直接写出所有点A移动的距离和方向;
(3)若A、B、C三个点移动后得到三个互不相等的有理数,它们既可以表示为1,
 ,
, 的形式,又可以表示为0,
的形式,又可以表示为0, ,
, 的形式,试求
的形式,试求 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=
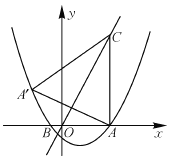
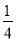 x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地举行龙舟赛,甲、乙两队在比赛时,路程
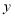 (米)与时间
(米)与时间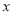 (分钟)的函数图象如图所示,根据函数图象填空和解答问题:
(分钟)的函数图象如图所示,根据函数图象填空和解答问题: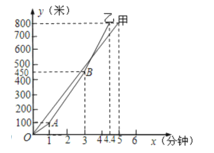
(1)最先到达终点的是_________队,比另一队领先_________分钟到达;
(2)在比赛过程中,甲队的速度始终保持为_________米/分;而乙队在第________分钟后第一次加速,速度变为_________米/分,在第__________分钟后第二次加速;
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
相关试题

