【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系![]() 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
参考答案:
【答案】解:(1)设抛物线的为y=ax2+11,由题意得B(8,8),∴64a+11=8,解得![]() 。
。
∴抛物线的解析式y=![]() x2+11。
x2+11。
(2)画出![]() 的图象:
的图象:
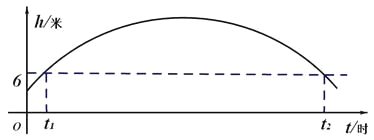
水面到顶点C的距离不大于5米时,即水面与河底ED的距离h≥6,
当h=6时,![]() ,解得t1=35,t2=3。
,解得t1=35,t2=3。
∴35-3=32(小时)。
答:需32小时禁止船只通行。
【解析】二次函数的应用,待定系数法,曲线上点的坐标与方程的关系。
(1)根据抛物线特点设出二次函数解析式,把B坐标代入即可求解。
(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至多为6,把6代入所给二次函数关系式,求得t的值,相减即可得到禁止船只通行的时间。
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:(a-2)2-(a-1)·(a+1)+5a,其中a=-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,抛物线
 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在
 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9,这5个数据的中位数是( )
A.6
B.7
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于
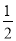 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
A. a=b B. 2a﹣b=1 C. 2a+b=﹣1 D. 2a+b=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
 =8,CD=
=8,CD= =2,
=2,此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
 =8,CD=
=8,CD= =2,
=2,此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y=
 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )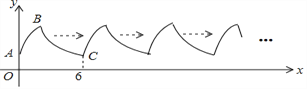
A. 72 B. 36 C. 16 D. 9
相关试题

