【题目】在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A. 3![]() B. 2
B. 2![]() C. 5 D. 6
C. 5 D. 6
参考答案:
【答案】D
【解析】分析:先根据B(3m,4m+1),可知B在直线y=![]() x+1上,所以当BD⊥直线y=
x+1上,所以当BD⊥直线y=![]() x+1时,BD最小,找一等量关系列关于m的方程,作辅助线:过B作BH⊥x轴于H,则BH=4m+1,利用三角形相似得BH2=EHFH,列等式求m的值,得BD的长即可.
x+1时,BD最小,找一等量关系列关于m的方程,作辅助线:过B作BH⊥x轴于H,则BH=4m+1,利用三角形相似得BH2=EHFH,列等式求m的值,得BD的长即可.
详解:如图,
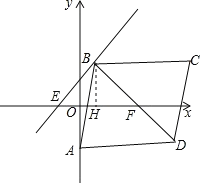
∵点B(3m,4m+1),
∴令![]() ,
,
∴y=![]() x+1,
x+1,
∴B在直线y=![]() x+1上,
x+1上,
∴当BD⊥直线y=![]() x+1时,BD最小,
x+1时,BD最小,
过B作BH⊥x轴于H,则BH=4m+1,
∵BE在直线y=![]() x+1上,且点E在x轴上,
x+1上,且点E在x轴上,
∴E(![]() ,0),G(0,1)
,0),G(0,1)
∵F是AC的中点
∵A(0,2),点C(6,2),
∴F(3,0)
在Rt△BEF中,
∵BH2=EHFH,
∴(4m+1)2=(3m+![]() )(33m),
)(33m),
解得:m1=![]() (舍),m2=
(舍),m2=![]() ,
,
∴B(![]() ,
,![]() ),
),
∴BD=2BF=2×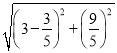 =6,
=6,
则对角线BD的最小值是6;
故答案为:6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
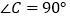 ,
,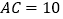 ,
,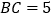 ,
,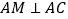 ,点
,点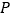 和点
和点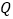 从
从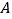 点出发,分别在射线
点出发,分别在射线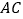 和射线
和射线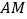 上运动,且
上运动,且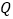 点运动的速度是
点运动的速度是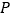 点运动的速度的
点运动的速度的 倍,当点
倍,当点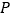 运动至__________时,
运动至__________时,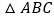 与
与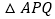 全等.
全等.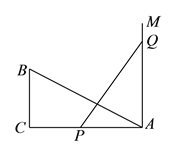
-
科目: 来源: 题型:
查看答案和解析>>【题目】(
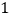 )如图①,在四边形
)如图①,在四边形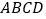 中,
中, ,
,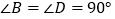 ,
,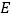 、
、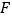 分别是边
分别是边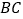 、
、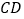 上的点,且
上的点,且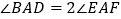 .
.求证:
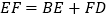 .
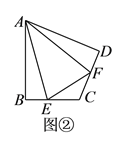
.(
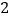 )如图②,在四边形
)如图②,在四边形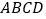 中,
中, ,
,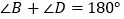 ,
,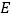 、
、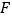 分别是边
分别是边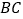 、
、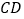 上的点,且
上的点,且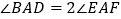 ,(
,(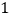 )中的结论是否仍然成立?
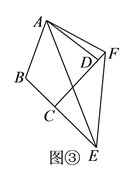
)中的结论是否仍然成立?(
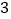 )如图③,在四边形
)如图③,在四边形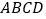 中,
中, ,
,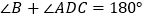 ,
,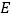 、
、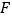 分别是边
分别是边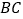 、
、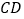 延长线上的点,且
延长线上的点,且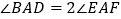 .(
.(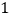 )中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.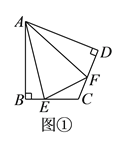
-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用题:
社会是一个重要的学校和课堂,生活是一种重要的课程和教材,实践是一种重要的学习方式和途径.参加社会生活和社会实践,不仅可以学到很多在课堂上学不到的东西,也可以把课堂上学到的理论知识同社会实践联系起来,加深对课堂学习内容的理解,我区某校七年级学生在农场进行社会实践活动时,采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:

(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
-
科目: 来源: 题型:
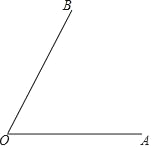
查看答案和解析>>【题目】如图,∠AOB=60°,分别引射线OC、OD、OE,使OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=20°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(其中α是小于60°的锐角),请直接写出∠BOE的度数(用含α的代数式表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
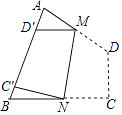
A.50°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】(新知理解)
如图①,点C在线段AB上,若BC=πAC,则称点C是线段AB的圆周率点,线段AC、BC称作互为圆周率伴侣线段.
(1)若AC=3,求AB;
(2)若点D也是图①中线段AB的圆周率点(不同于点C),判断AC,BD的等量关系;
(解决问题)
如图②,现有一个直径为1个单位长度的圆片,将圆片上的某点与数轴上表示1的点重合,并把圆片沿数轴向右无滑动地滚动1周,该点到达点C的位置.
(3)若点M、N是线段OC的圆周率点,求MN的长;
(4)图②中,若点D在射线OC上,且线段CD与以O、C、D中某两个点为端点的线段互为圆周率伴侣线段,请直接写出点D所表示的数.

相关试题

