【题目】(![]() )如图①,在四边形
)如图①,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() .
.
求证:![]() .
.
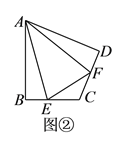
(![]() )如图②,在四边形
)如图②,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() ,(
,(![]() )中的结论是否仍然成立?
)中的结论是否仍然成立?
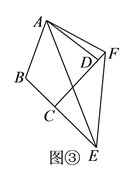
(![]() )如图③,在四边形
)如图③,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 延长线上的点,且
延长线上的点,且![]() .(
.(![]() )中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
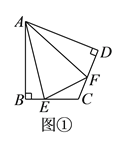
参考答案:
【答案】见解析
【解析】(1)可通过构建全等三角形来实现线段间的转换.延长EB到G,使BG=DF,连接AG.目的就是要证明三角形AGE和三角形AEF全等将EF转换成GE,那么这样EF=BE+DF了,于是证明两组三角形全等就是解题的关键.三角形ABE和AEF中,只有一条公共边AE,我们就要通过其他的全等三角形来实现,在三角形ABG和AFD中,已知了一组直角,BG=DF,AB=AD,因此两三角形全等,那么AG=AF,∠1=∠2,那么∠1+∠3=∠2+∠3=∠EAF=![]() ∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.
∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.
(2)思路和作辅助线的方法与(1)完全一样,只不过证明三角形ABG和ADF全等中,证明∠ABG=∠ADF时,用到的等角的补角相等,其他的都一样.因此与(1)的结果完全一样.
(3)按照(1)的思路,我们应该通过全等三角形来实现相等线段的转换.就应该在BE上截取BG,使BG=DF,连接AG.根据(1)的证法,我们可得出DF=BG,GE=EF,那么EF=GE=BE-BG=BE-DF.所以(1)的结论在(3)的条件下是不成立的.
(![]() )延长
)延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(![]() )(
)(![]() )中的结论仍成立,
)中的结论仍成立,
证明:延长![]() 至点
至点![]() ,使
,使![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
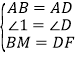 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 即
即![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,即
,即![]() .
.
(![]() )结论不成立,应当是
)结论不成立,应当是![]() ,
,
证明:在![]() 上截取
上截取![]() 使
使![]() ,
,
连接![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
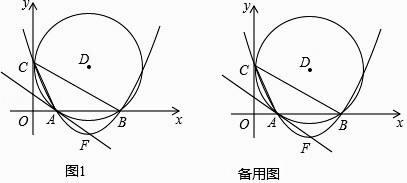
(1)D点的坐标是 , 圆的半径为;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大面积是多少?并求出N点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国传统数学最重要的著作,其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:有几个人共同出钱买鸡?鸡的价钱是多少?”设有x个人共同买鸡,根据题意列一元一次方程,正确的是( )

A. 9x﹣11=6x+16 B. 9x+11=6x﹣16 C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
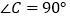 ,
,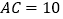 ,
,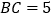 ,
,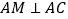 ,点
,点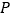 和点
和点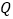 从
从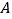 点出发,分别在射线
点出发,分别在射线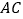 和射线
和射线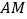 上运动,且
上运动,且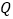 点运动的速度是
点运动的速度是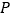 点运动的速度的
点运动的速度的 倍,当点
倍,当点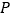 运动至__________时,
运动至__________时,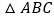 与
与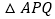 全等.
全等.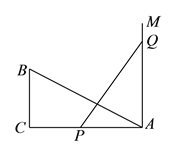
-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用题:
社会是一个重要的学校和课堂,生活是一种重要的课程和教材,实践是一种重要的学习方式和途径.参加社会生活和社会实践,不仅可以学到很多在课堂上学不到的东西,也可以把课堂上学到的理论知识同社会实践联系起来,加深对课堂学习内容的理解,我区某校七年级学生在农场进行社会实践活动时,采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:

(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A. 3
 B. 2
B. 2 C. 5 D. 6
C. 5 D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=60°,分别引射线OC、OD、OE,使OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=20°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(其中α是小于60°的锐角),请直接写出∠BOE的度数(用含α的代数式表示).
相关试题

