【题目】如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8. 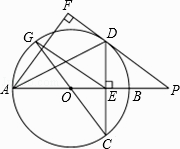
(1)求证:DF是⊙O的切线;
(2)求证:OC2=OEOP;
(3)求线段EG的长.
参考答案:
【答案】
(1)证明:连接OD,如图1所示:
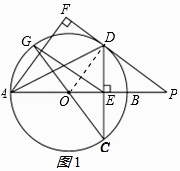
∵OA=OD,
∴∠DAB=∠ADO,
∵∠DAF=∠DAB,
∴∠ADO=∠DAF,
∴OD//AF,
又∵DF⊥AF,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)证明:由(1)得:DF⊥OD,
∴∠ODF=90°,
∵AB⊥CD,
∴由射影定理得:OD2=OEOP,
∵OC=OD,
∴OC2=OEOP
(3)解:连接DG,如图2所示:
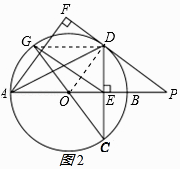
∵AB⊥CD,
∴DE=CE=4,
∴CD=DE+CE=8,
设OD=OA=x,则OE=8﹣x,
在Rt△ODE中,由勾股定理得:OE2+DE2=OD2,
即(8﹣x)2+42=x2,
解得:x=5,
∴CG=2OA=10,
∵CG是⊙O的直径,
∴∠CDG=90°,
∴DG= ![]() =
= ![]() =6,
=6,
∴EG= ![]() =
= ![]() =2
=2 ![]() .
.
【解析】(1)连接OD,由等腰三角形的性质得出∠DAB=∠ADO,再由已知条件得出∠ADO=∠DAF,证出OD//AF,由已知DF⊥AF,得出DF⊥OD,即可得出结论;(2)由射影定理得出OD2=OEOP,由OC=OD,即可得出OC2=OEOP;(3)连接DG,由垂径定理得出DE=CE=4,得出CD=8,由勾股定理求出DG,再由勾股定理求出EG即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明想探究函数
 的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:x
…
-3
-2
-1
1
2
3
…
y
…
2.83
1.73
0
0
1.73
2.83
…
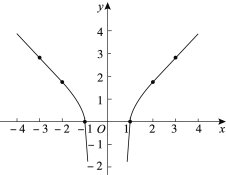
小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:小聪判断的理由是_____________.请写出函数
 的一条性质:_____________.
的一条性质:_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线
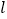 的表达式为
的表达式为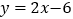 ,点A,B的坐标分别为
,点A,B的坐标分别为(1,0),(0,2),直线AB与直线
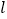 相交于点P.
相交于点P.(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线
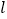 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.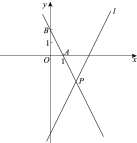
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下表三行数的规律,回答下列问题:
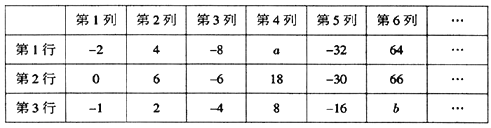
(1)第1行的第四个数a是多少;第3行的第六个数b是多少;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为多少;
(3)巳知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
-
科目: 来源: 题型:
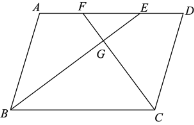
查看答案和解析>>【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由大小相同(棱长为1分米)的小立方块搭成的几何体如下图.


(1)请在右图的方格中画出该几何体的俯视图和左视图;
(2)图中有 块小正方体,它的表面积(含下底面)为 ;
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要_______个小立方块,最多要_______个小立方块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调查分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
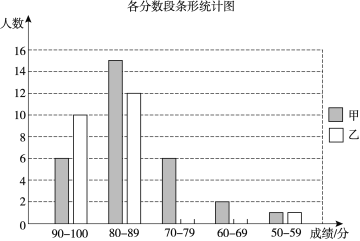
(1)请根据乙校的数据补全条形统计图;
(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数
中位数
众数
甲校
83.4
87
89
乙校
83.2
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,
请为他们各写出一条可以使用的理由;
甲校: .乙校: .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .
相关试题

