【题目】如图①,正方形ABCD中,点A,B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D→A匀速运动,同时动点Q以相同的速度在x轴正半轴上运动,当点P到达A点时,两点同时停止运动,设运动的时间为t秒.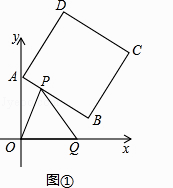
(1)当P点在边AB上运动时点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;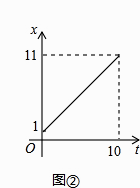
(2)求正方形边长及顶点C的坐标;
(3)在(1)中,设△OPQ的面积为S,求S与t的函数关系式并写出自变量的取值范围.
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等?若能,写出所有符合条件的t的值;若不能,请说明理由.
参考答案:
【答案】
(1)
解:如图①,过B作BF⊥OA于F,

∵A(0,10),
∴OA=10,
∵B(8,4),
∴BF=8,OF=4,
∴AF=10﹣4=6,
∴AB=10,
由图②知:点P在边AB上运动时间为10秒,所以速度为:10÷10=1,
Q(1,0),
则点P运动速度为每秒1个单位长度;
(2)
解:如图③,过B作BF⊥y轴于点F,BE⊥x轴于点E,则BF=8,OF=BE=4,

由(1)知:AF=6,AB=10;
过C作CG⊥x轴于点G,与FB的延长线交于点H,
∵∠ABC=90°,AB=BC,
∴△ABF≌△BCH,
∴BH=AF=6,CH=BF=8,
∴OG=FH=8+6=14,CG=8+4=12,
∴所求C点的坐标为(14,12);
(3)
解:过点P作PM⊥y轴于点M,PN⊥x轴于点N,

∴PM∥BF,
则△APM∽△ABF,
∴ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AM= ![]() ,PM=
,PM= ![]() t,
t,
∴PN=OM=10﹣ ![]() t,ON=PM=
t,ON=PM= ![]() t,
t,
∴S=S△OPQ= ![]() PNOQ
PNOQ
= ![]() ×(10﹣
×(10﹣ ![]() t)(1+t)=﹣
t)(1+t)=﹣ ![]() (0≤t≤10);
(0≤t≤10);
(4)
解:OP与PQ相等,组成等腰三角形,即当P点的横坐标等于Q点的横坐标的一半时,满足条件;
①当P在AB上时,如图③, ![]() t=
t= ![]() (t+1),t=
(t+1),t= ![]() ,OP与PQ相等,
,OP与PQ相等,

②当P在BC上时,如图④,则PB=t﹣10,

sin∠ABF=sin∠BPM= ![]() ,
,
∴ ![]() ,
,
∴BM= ![]() (t﹣10),
(t﹣10),
∴ON=BF+BM=8+ ![]() (t﹣10),
(t﹣10),
8+ ![]() (t﹣10)=
(t﹣10)= ![]() (t+1),解得:t=﹣15(舍),
(t+1),解得:t=﹣15(舍),
③当P在CD上时,如图⑤,则PC=t﹣20,
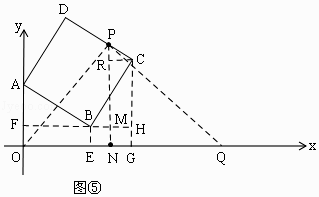
cos∠PCR=cos∠BCH= ![]() ,
,
∴ ![]() ,
,
∴CR=MH= ![]() (t﹣20),
(t﹣20),
∴ON=OG﹣NG=FH﹣MH=14﹣ ![]() (t﹣20),
(t﹣20),
14﹣ ![]() (t﹣20)=
(t﹣20)= ![]() (t+1),解得:t=
(t+1),解得:t= ![]() ,
,
即当t= ![]() 时,OP=PQ,
时,OP=PQ,
综上所述,当t= ![]() 或
或 ![]() 时,OP与PQ相等.
时,OP与PQ相等.
【解析】(1)由A和B两点的坐标求正方形边长AB,由图②得:P在边AB上运动10秒,Q开始运动时,横坐标为1;(2)由(1)知,正方形边长为10,根据三角形全等得:BH=AF=6,CH=BF=8,所以可得OG=14,CG=12,写出C点的坐标;(3)作辅助线,证明△APM∽△ABF,列比例式得:AM= ![]() ,PM=
,PM= ![]() t,根据面积公式可得S与t的关系式;(4)OP与PQ相等,组成等腰三角形,即当P点的横坐标等于Q点的横坐标的一半;分三种情况进行讨论:点P分别在AB、BC、CD上时,根据这一等量关系列式可得t的值.
t,根据面积公式可得S与t的关系式;(4)OP与PQ相等,组成等腰三角形,即当P点的横坐标等于Q点的横坐标的一半;分三种情况进行讨论:点P分别在AB、BC、CD上时,根据这一等量关系列式可得t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=120°,OC⊥OB,按下列要求利用量角器过点O作出射线OD、OE;
(1)在图①中作出射线OD满足∠COD=50°,并直接写出∠AOD的度数是 ;
(2)在图②中作出射线OD、OE,使得OD平分∠AOC,OE平分∠BOD,并求∠COE的度数;
(3)如图③,若射线OD从OA出发以每秒10°的速度绕点O顺时针方向旋转,同时射线OE从OC出发以每秒5°的速度绕点O顺时针方向旋转,设旋转的时间为t秒,在旋转过程中,当OB第一次恰好平分∠DOE时,求出t的值,并作出此时OD、OE的大概位置.

-
科目: 来源: 题型:
查看答案和解析>>【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种水果80千克的钱,现在可买88千克.
(1)现在实际购进这种水果每千克多少元?
(2)王阿姨准备购进这种水果销售,若这种水果的销售量y(千克)与销售单价x(元/千克)满足如图所示的一次函数关系. ①求y与x之间的函数关系式;
②请你帮王阿姨拿个主意,将这种水果的销售单价定为多少时,能获得最大利润?最大利润是多少?(利润=销售收入﹣进货金额)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,1),直线l:y=﹣1.动点P满足条件:
①P在这个平面直角坐标系中;
②P到A的距离和P到l的距离相等;
(1)求点P所经过的轨迹方程,并在网格中绘制这个图象.(提示:平面直角坐标系中两点之间的距离可以通过勾股定理来求得)
(2)已知直线y=kx+1,小明同学说,这条直线与(1)中所绘的图象有两个交点?你能说明小明为什么这么说吗?
(3)经过了上述的计算、绘图,小明发现,如果第(2)问的两个交点分别为B、C,那么,过BC的中点M作直线l的垂线,垂足为H,连接BH、CH,所得到的三角形BCH是个特殊的三角形,你能说明它是什么三角形吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将形状、大小完全相同的“
 ”和线段按照一定规律摆成下列图形.第1幅图形中“
”和线段按照一定规律摆成下列图形.第1幅图形中“ ”的个数为
”的个数为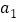 ,第2幅图形中“
,第2幅图形中“ ”的个数为
”的个数为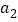 ,第3幅图形中“
,第3幅图形中“ ”的个数为
”的个数为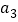 ,……,以此类推,解决以下问题:
,……,以此类推,解决以下问题:(1)直接写出
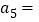 ,
,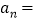 (用含n的代数式表示);
(用含n的代数式表示);(2)猜想是否存在某幅图中“
 ”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;
”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;(3)求出
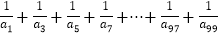 的值.
的值.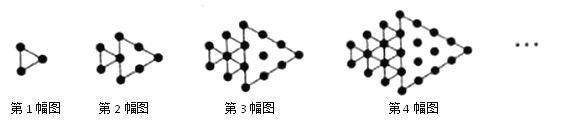
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段达到节水的目的,右下表是调控后的价目表.
(1)若该户居民8月份用水8吨,则该用户8月应交水费 元;若该户居民9月份应交水费26元,则该用户9月份用水量 吨;
(2)若该户居民10月份应交水费30元,求该用户10月份用水量;
(3)若该户居民11月、12月共用水18吨,共交水费52元,求11月、12月各应交水费多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).

(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
相关试题

