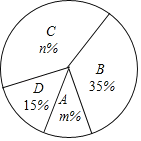
【题目】今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩(s) | 频数(人数) |
A | 90<s≤100 | 4 |
B | 80<s≤90 | x |
C | 70<s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息,解答以下问题:
(1)表中的x= ;
(2)扇形统计图中m= ,n= ,C等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.
参考答案:
【答案】(1)14;(2)10、40、144;(3)恰好选取的是a1和b1的概率为![]() .
.
【解析】(1)根据D组人数及其所占百分比可得总人数,用总人数减去其他三组人数即可得出x的值;
(2)用A、C人数分别除以总人数求得A、C的百分比即可得m、n的值,再用360°乘以C等级百分比可得其度数;
(3)首先根据题意列出表格,然后由表格求得所有等可能的结果与恰好选取的是a1和b1的情况,再利用概率公式即可求得答案.
(1)∵被调查的学生总人数为6÷15%=40人,
∴x=40﹣(4+16+6)=14,
故答案为:14;
(2)∵m%=![]() ×100%=10%,n%=
×100%=10%,n%=![]() ×10%=40%,
×10%=40%,
∴m=10、n=40,
C等级对应的扇形的圆心角为360°×40%=144°,
故答案为:10、40、144;
(3)列表如下:
a1 | a2 | b1 | b2 | |
a1 | a2,a1 | b1,a1 | b2,a1 | |
a2 | a1,a2 | b1,a2 | b2,a2 | |
b1 | a1,b1 | a2,b1 | b2,b1 | |
b2 | a1,b2 | a2,b2 | b1,b2 |
由表可知共有12种等可能结果,其中恰好选取的是a1和b1的有2种结果,
∴恰好选取的是a1和b1的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD,CE是角平分线,则图中的等腰三角形共有
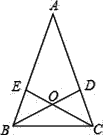
A. 8个 B. 7个 C. 6个 D. 5个
-
科目: 来源: 题型:
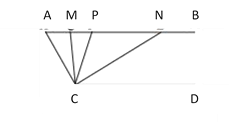
查看答案和解析>>【题目】如图,已知AB∥CD,∠A=40°,点P是射线B上一动点(与点A不重合),CM,CN分别平分∠ACP和∠PCD,分别交射线AB于点M,N.
(1)求∠MCN的度数.
(2)当点P运动到某处时,∠AMC=∠ACN,求此时∠ACM的度数.
(3)在点P运动的过程中,∠APC与∠ANC的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
-
科目: 来源: 题型:
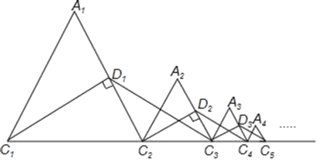
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnnCn+1的周长和为_____.(n≥2,且n为整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
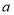 、
、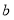 、
、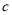 在数轴上的位置如图所示,回答下列问题:
在数轴上的位置如图所示,回答下列问题:
(1)化简:
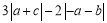 ;
; (2)令
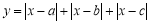 ,请问
,请问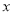 满足什么条件时,
满足什么条件时,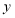 有最小值,并求出该最小值.
有最小值,并求出该最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
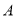 地某厂和
地某厂和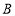 地某厂同时制成机器若干台,
地某厂同时制成机器若干台,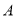 地某厂可支援外地
地某厂可支援外地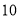 台,
台,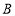 地某厂可支援外地
地某厂可支援外地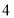 台,现决定给
台,现决定给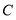 地
地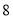 台,
台,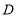 地
地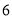 台,已知从
台,已知从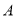 运往
运往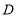 、
、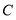 两地的运费分别是
两地的运费分别是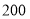 元每台、
元每台、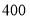 元每台,从
元每台,从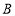 运往
运往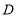 、
、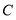 两地的运费分别是
两地的运费分别是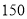 元每台、
元每台、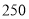 元每台.
元每台.(1)设
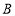 地某厂运往
地某厂运往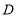 地
地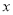 台,求总运费为多少元?
台,求总运费为多少元? (2)在(1)中,当
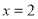 时,总运费是多少元?
时,总运费是多少元?
相关试题

