【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。
(1)求抛物线的解析式。
(2)求△ABC的面积。若P是抛物线上一点(异于点C),且满足△ABP的面积等于△ABC的面积,求满足条件的点P的坐标。
(3)点M是线段BC上的点(不与B , C重合),过M作MN∥ ![]() 轴交抛物线于N , 若点M的横坐标为
轴交抛物线于N , 若点M的横坐标为 ![]() ,请用含
,请用含 ![]() 的代数式表示线段MN的长。
的代数式表示线段MN的长。
(4)在(3)的条件下,连接NB、NC , 则是否存在点M,使△BNC的面积最大?若存在,求 ![]() 的值,并求出△BNC面积的最大值。若不存在,说明理由。
的值,并求出△BNC面积的最大值。若不存在,说明理由。
参考答案:
【答案】
(1)解:由已知条件可设抛物线解析式为 ![]() ,
,
∵点C(0,3)在抛物线上.
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为 ![]() .
.
(2)解:∵点A、B、C的坐标分别为:A(-1,0)、B(3,0)、C(0,3),
∴AB=4,OC=3
∴ S△ABC= ![]() ,
,
设点P的坐标为 ![]() ,
,
∵ S△ABP= S△ABC=6,
∴点P纵坐标的绝对值等于OC的长,即: ![]()
当-x2+2x+3.=3时,解得 ![]()
∴P(0,3)(舍), P(2,3)
当-x2+2x+3.=-3时,解得 ![]()
∴P( ![]() ,-3), P(
,-3), P( ![]() ,-3)
,-3)
∴满足条件的点P的坐标为(2,3)( ![]() ,-3)(
,-3)( ![]() ,-3)
,-3)
(3)解:如图1,设MN交x轴于点D,
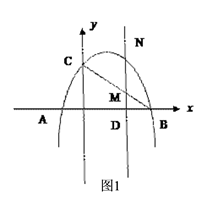
∵MN∥y轴,点M横坐标为m,
∴N的横坐标为m, D(m,0)
∵点N在抛物线上
∴点N的坐标为N( m, -m2+2m+3),
设直线BC解析式为y=kx+b,
∴ ![]() 解得
解得 ![]()
∴直线BC的解析式为y= -x+3.
∵点M在直线BC上,
∴点M(m, -m+3)
∴MN=DN-DM=(-m2+2m+3)-(-m+3)=-m2+3m
(4)解:存在.如2,连接BN、CN
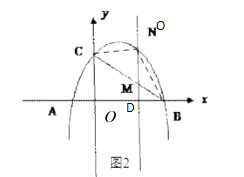
设△BNC的面积为S,则
![]()
∵ ![]() ,且
,且 ![]() ,
,
∴ ![]() 时,△BNC的面积最大,最大面积为
时,△BNC的面积最大,最大面积为 ![]() .
.
【解析】(1)根据已知点的特点,设二次函数解析式为交点式,再将点C的坐标代入即可求出函数解析式。
(2)先根据点A、B、C的坐标分别求出AB、OC的长,再根据三角形的面积公式即可求得结果;根据已知△ABP的面积等于△ABC的面积,而AB=4, S△ABC= 6 ,可求出△ABP的AB边上的高为3,即点P的纵坐标的绝对值等于3,设点P的坐标,根据点P的纵坐标=±3,建立方程,求解即可求出点P的坐标。
(3)根据已知MN∥y轴,交抛物线与N,根据点M的横坐标表示出点N的坐标,点D的坐标,再求出直线BC的函数解析式,就可表示出点M的坐标,然后用含m的代数式分别表示出DN、DM的长,即可求出MN关于m的函数解析式。
(4)连接BN、CN,根据△BNC的面积=△BMN的面积+△MNC的面积,△BMN和△MNC有公共的底边,两三角形的高之和为OB的长,可建立s与m的函数解析式,求出顶点坐标,即可得出结论。
【考点精析】利用二次函数图象的平移和二次函数的最值对题目进行判断即可得到答案,需要熟知平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小赵为班级购买笔记本作为晚会上的奖品回来时向生活委员交账说:“一共买了
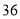 本,有两种规格,单价分别为
本,有两种规格,单价分别为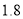 元和
元和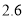 元去时我领了
元去时我领了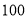 元,现在找回
元,现在找回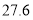 元”生活委员算了一下,认为小赵搞错了.
元”生活委员算了一下,认为小赵搞错了.(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起 当做找回的钱给了生活委员.如果设购买单价为
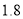 元的笔记本
元的笔记本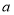 本,试用含
本,试用含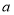 的代数式表示小赵零用钱的数目: 元
的代数式表示小赵零用钱的数目: 元(3)如果小赵的零用钱数目是整数,且少于
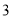 元,试求出小赵零用钱的数目.
元,试求出小赵零用钱的数目. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是用棋子成的T字形图案:
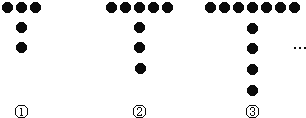
(1)填写下表:
图案序号
①
②
③
④
……
⑧
每个图案中棋子的个数
5
8
……
(2)第
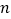 个“T“字形图案中棋子的个数为多少 (用含
个“T“字形图案中棋子的个数为多少 (用含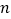 的代数式表示);
的代数式表示);(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.
-
科目: 来源: 题型:
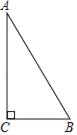
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4.
(1)若BC=2,求AB的长;
(2)若BC=a,AB=c,求代数式(c﹣2)2﹣(a+4)2+4(c+2a+3)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).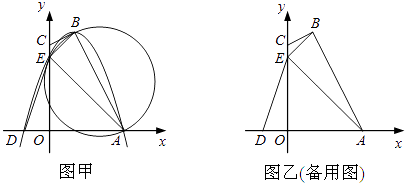
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知一次函数y=﹣
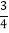 x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )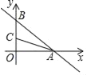
A. (0,3) B. (0,
 ) C. (0,
) C. (0, ) D. (0,
) D. (0, )
)
相关试题

