【题目】如图所示的是用棋子成的T字形图案:
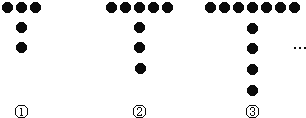
(1)填写下表:
图案序号 | ① | ② | ③ | ④ | …… | ⑧ |
每个图案中棋子的个数 | 5 | 8 | …… |
(2)第![]() 个“T“字形图案中棋子的个数为多少 (用含
个“T“字形图案中棋子的个数为多少 (用含![]() 的代数式表示);
的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.
参考答案:
【答案】(1)11,14,26 (2)3n+2 (3)62 (4)670
【解析】
(1)通过观察已知图形可得:每个图形都比其前一个图形多3枚棋子,得出摆成第③④⑧个图形需要的棋子数;
(2)由(1)得出规律为摆成第n个图形需要(3n+2)个棋子;
(3)将n=20代入(2)中规律计算即可求解;
(4)由(2)中规律求解即可.
解:(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.即第n个图案需要5+3(n-1)=3n+2.那么当n=3时,则有11枚;当n=4时,则有14枚;当n=8时,则有26枚;
填表如下:
图形序号 | ① | ② | ③ | ④ | … | ⑧ |
每个图案中棋子个数 | 5 | 8 | 11 | 14 | … | 26 |
(2)因为第①个图案有5枚棋子,
第②个图案有(5+3×1)枚棋子,
第③个图案有(5+3×2)枚棋子,
依此规律可得第n个图案需5+3×(n-1)=5+3n-3=(3n+2)枚棋子.
(3)第20个“T”字形图案共有棋子3×20+2=62(个).
即第20个图案需62个棋子;
(4)前20个“T”字形图案中棋子的总个数为:
5+8+11+14+17+…+53+56+59+62
=(5+62)+(8+59)+(11+56)+…+(32+35)
=67×10
=670(个).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小赵为班级购买笔记本作为晚会上的奖品回来时向生活委员交账说:“一共买了
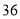 本,有两种规格,单价分别为
本,有两种规格,单价分别为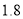 元和
元和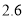 元去时我领了
元去时我领了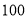 元,现在找回
元,现在找回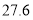 元”生活委员算了一下,认为小赵搞错了.
元”生活委员算了一下,认为小赵搞错了.(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起 当做找回的钱给了生活委员.如果设购买单价为
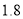 元的笔记本
元的笔记本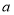 本,试用含
本,试用含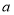 的代数式表示小赵零用钱的数目: 元
的代数式表示小赵零用钱的数目: 元(3)如果小赵的零用钱数目是整数,且少于
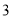 元,试求出小赵零用钱的数目.
元,试求出小赵零用钱的数目. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。

(1)求抛物线的解析式。
(2)求△ABC的面积。若P是抛物线上一点(异于点C),且满足△ABP的面积等于△ABC的面积,求满足条件的点P的坐标。
(3)点M是线段BC上的点(不与B , C重合),过M作MN∥ 轴交抛物线于N , 若点M的横坐标为
轴交抛物线于N , 若点M的横坐标为  ,请用含
,请用含  的代数式表示线段MN的长。
的代数式表示线段MN的长。
(4)在(3)的条件下,连接NB、NC , 则是否存在点M,使△BNC的面积最大?若存在,求 的值,并求出△BNC面积的最大值。若不存在,说明理由。
的值,并求出△BNC面积的最大值。若不存在,说明理由。 -
科目: 来源: 题型:
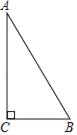
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4.
(1)若BC=2,求AB的长;
(2)若BC=a,AB=c,求代数式(c﹣2)2﹣(a+4)2+4(c+2a+3)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).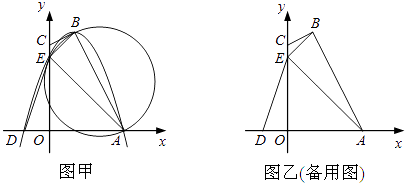
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
相关试题

