【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
参考答案:
【答案】
(1)解:由题意可得:(1)y=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
=-5x2+800x-27500
∴ ![]() 与
与 ![]() 之间的函数关系为:
之间的函数关系为: ![]() .
.
(2)解:y=-5x2+800x-27500
=-5(x-80)2+4500
∵a=-5<0,
∴抛物线开口向下.
∵50≤ ![]() ≤100,对称轴是直线
≤100,对称轴是直线 ![]() =80,
=80,
∴当 ![]() =80时,
=80时, ![]() 最大=4500.
最大=4500.
(3)解:当 ![]() =4000时,-5(
=4000时,-5( ![]() -80)2+4500=4000,解得
-80)2+4500=4000,解得 ![]() =70,
=70, ![]() =90,
=90,
又∵ ![]() 的图象开口向下,
的图象开口向下,
∴当70≤ ![]() ≤90时,每天的销售利润不低于4000元.
≤90时,每天的销售利润不低于4000元.
由每天的总成本不超过7000元,得50(-5 ![]() +550)≤7000,解得
+550)≤7000,解得 ![]() ≥82,
≥82,
∴82≤ ![]() ≤90,
≤90,
∵50≤ ![]() ≤100,
≤100,
∴销售单价应该控制在82元至90元(包括端点)之间.
【解析】(1)根据每天的销售利润y=每一件的利润![]() 每天的销售量,即可求出函数解析式。
每天的销售量,即可求出函数解析式。
(2)求出(1)中函数的顶点坐标,即可求出结论。
(3)先求出y=4000时对应的自变量x的值,结合二次函数的性质,得出每天的销售利润不低于4000元时自变量的取值范围;再根据每天的总成本≤7000,建立不等式求解,即可求出销售单价应控制的范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )

A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小赵为班级购买笔记本作为晚会上的奖品回来时向生活委员交账说:“一共买了
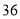 本,有两种规格,单价分别为
本,有两种规格,单价分别为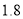 元和
元和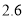 元去时我领了
元去时我领了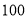 元,现在找回
元,现在找回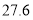 元”生活委员算了一下,认为小赵搞错了.
元”生活委员算了一下,认为小赵搞错了.(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起 当做找回的钱给了生活委员.如果设购买单价为
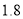 元的笔记本
元的笔记本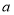 本,试用含
本,试用含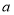 的代数式表示小赵零用钱的数目: 元
的代数式表示小赵零用钱的数目: 元(3)如果小赵的零用钱数目是整数,且少于
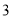 元,试求出小赵零用钱的数目.
元,试求出小赵零用钱的数目. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的是用棋子成的T字形图案:
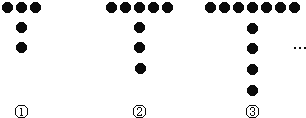
(1)填写下表:
图案序号
①
②
③
④
……
⑧
每个图案中棋子的个数
5
8
……
(2)第
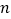 个“T“字形图案中棋子的个数为多少 (用含
个“T“字形图案中棋子的个数为多少 (用含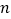 的代数式表示);
的代数式表示);(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点。

(1)求抛物线的解析式。
(2)求△ABC的面积。若P是抛物线上一点(异于点C),且满足△ABP的面积等于△ABC的面积,求满足条件的点P的坐标。
(3)点M是线段BC上的点(不与B , C重合),过M作MN∥ 轴交抛物线于N , 若点M的横坐标为
轴交抛物线于N , 若点M的横坐标为  ,请用含
,请用含  的代数式表示线段MN的长。
的代数式表示线段MN的长。
(4)在(3)的条件下,连接NB、NC , 则是否存在点M,使△BNC的面积最大?若存在,求 的值,并求出△BNC面积的最大值。若不存在,说明理由。
的值,并求出△BNC面积的最大值。若不存在,说明理由。 -
科目: 来源: 题型:
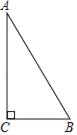
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4.
(1)若BC=2,求AB的长;
(2)若BC=a,AB=c,求代数式(c﹣2)2﹣(a+4)2+4(c+2a+3)的值.
相关试题

