【题目】在菱形ABCD中,∠B=60,E是边CD上一点,以CE为边作等边△CEF.
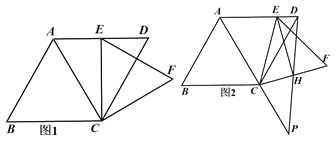
(1) 如图1,当CE⊥AD ,CF=![]() 时,求菱形ABCD的面积;
时,求菱形ABCD的面积;
(2) 如图2,过点E作∠CEF的平分线交CF于H,连接DH,并延长DH与AC的延长交于点P,若∠ECD=15,求证:![]() .
.
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由等边三角形的性质得出CE的长.再由菱形的性质及∠B=60得到CD的长,根据菱形的面积公式即可得出结论.
(2)连接DF,过F作FG⊥CD于G.由菱形的性质及∠B=60得到△ABC和△ACD是等边三角形,即可证明△ACE≌△DCF,进而得到DF//AP,由平行线的性质得到∠FDH=∠CPH.
由等边三角形的性质得到CH=HF.可证明△CHP≌△FHD,得到DF=CP.在Rt△DGF中,由∠FDC=60,可得![]() .在等腰Rt△CFG中,有
.在等腰Rt△CFG中,有![]() ,从而可以得出结论.
,从而可以得出结论.
(1)∵等边△CEF,CF=![]() ,∴CE=CF=
,∴CE=CF=![]() .
.
∵菱形ABCD,∠B=60,∴∠D=∠B=60,AD=CD.
∵CE⊥AD,∴∠ECD=30,∴CD=4,∴AD=4,∴S菱形ABCD=ADCE=![]() .
.
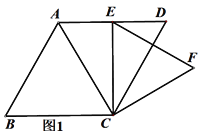
(2)连接DF,过F作FG⊥CD于G.
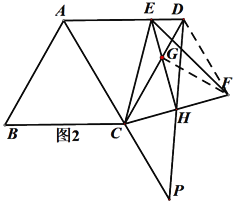
∵菱形ABCD,∴AB=BC=CD=AD.
∵∠B=60,∴△ABC和△ACD是等边三角形,∴∠CAD=∠ACD=60.
∵等边△CEF,∴CE=CF,∠ECF=60,∴∠ACD-∠ECD=∠ECF-∠ECD即∠ACE=∠DCF.
在△ACE与△DCF中,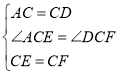 ,∴△ACE≌△DCF,∴∠FDC=60.
,∴△ACE≌△DCF,∴∠FDC=60.
∵∠ACD=60,∴DF//AP,∴∠FDH=∠CPH.
∵等边△CEF,EH平分∠CEF,∴CH=HF.
在△CHP与△FHD中,∵∠FDH=∠CPH,∠FHD=∠CHP,HF=CH,∴△CHP≌△FHD,∴DF=CP.
∵∠FDC=60,FG⊥CD,∴![]() .
.
∵∠ECF=60,∠ECD=15,∴∠DCF=45.
∵∠DCF=45,FG⊥CD,∴![]() ,∴
,∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表格给出的信息,探究y与x的关系:
x
-4
-3
-2
-1
0
1
2
3
4
y
4
3
2
1
0
1
2
3
4
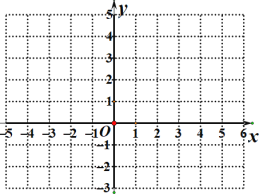
(1)写出y与x的函数关系式为____________;
(2)在下面的平面直角坐标系中,画出该函数的图象;
(3)根据图象说出y随x的变化规律,若函数y的值有最大(或小)值,直接写出y的最大(或小)值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
材料1:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号.如:
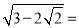
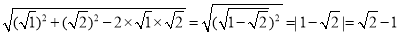 ;
;材料2: 配方法是初中数学思想方法中的一种重要的解题方法。配方法的最终目的就是配成完全平方式,利用完全平方式来解决问题。它的应用非常广泛,在解方程、求最值、证明等式、化简根式、因式分解等方面都经常用到。
如:
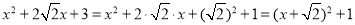
∵
 ,∴
,∴ 即
即
∴
 的最小值为1.
的最小值为1.根据以上材料解决下列问题:
(1)填空:
 =________________;
=________________;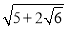 =______________;
=______________;(2)求
 的最小值;
的最小值;(3)已知
 ,求
,求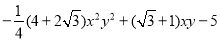 的最大值.
的最大值. -
科目: 来源: 题型:
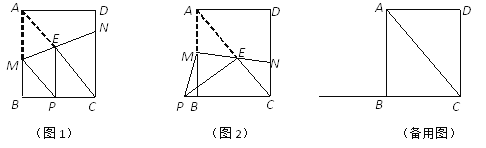
查看答案和解析>>【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线y=ax2﹣
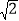 ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB
ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB(1)求这条抛物线的解析式及直线BC的解析式;
(2)设点D为抛物线对称轴上的一点,当点D在对称轴上运动时,是否可以与点C,A,B三点,构成梯形的四个顶点?若可以,求出点D坐标,若不可以,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
-
科目: 来源: 题型:
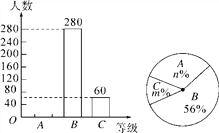
查看答案和解析>>【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)这次调查的市民人数为________人,m=________,n=________;
(2)补全条形统计图;
(3)若该市约有市民100000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.
相关试题

