【题目】已知,抛物线y=ax2﹣![]() ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB
ax﹣4a与x轴交于A,B两点,与y轴交于C点,A点在B点左侧,C点在x轴下方,且△AOC∽△COB
(1)求这条抛物线的解析式及直线BC的解析式;
(2)设点D为抛物线对称轴上的一点,当点D在对称轴上运动时,是否可以与点C,A,B三点,构成梯形的四个顶点?若可以,求出点D坐标,若不可以,请说明理由.
参考答案:
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2,y=
x﹣2,y=![]() x﹣2;(2)见解析
x﹣2;(2)见解析
【解析】分析:(1)将函数解析式变形为y=a(x-2![]() )(x+
)(x+![]() )可得A、B坐标,由解析式知C(0,-4a),根据△AOC∽△COB知
)可得A、B坐标,由解析式知C(0,-4a),根据△AOC∽△COB知![]() ,据此求得a的值,进一步可得抛物线和直线BC解析式;
,据此求得a的值,进一步可得抛物线和直线BC解析式;
(2)分CD1∥AB、AD2∥BC、BD3∥AC三种情况,利用相似三角形的性质分别求解可得答案.
详解:(1)∵y=ax2﹣![]() x﹣4a=a(x﹣2
x﹣4a=a(x﹣2![]() )(x+
)(x+![]() ),
),
∴由a(x﹣2![]() )(x+
)(x+![]() )=0且a≠0可得x=2
)=0且a≠0可得x=2![]() 或x=
或x=![]() ,
,
由题意知点A(﹣![]() ,0)、B(2
,0)、B(2![]() ,0),
,0),
当x=0时,y=﹣4a,
∴点C(0,﹣4a),
∵C点在x轴下方,
∴﹣4a<0,a>0,
如图1所示,
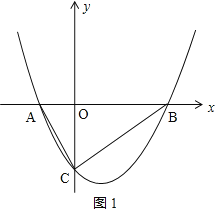
∵△AOC∽△COB,
∴![]() ,即
,即![]() ,
,
解得:a=﹣![]() (舍)或a=
(舍)或a=![]() ,
,
则抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣2,点C坐标为(0,﹣2),
x﹣2,点C坐标为(0,﹣2),
设直线BC解析式为y=kx+b,
将B(2![]() ,0)、C(0,﹣2)代入,得:
,0)、C(0,﹣2)代入,得:![]() ,
,
解得: ,
,
∴直线BC解析式为y=![]() x﹣2;
x﹣2;
(2)抛物线的对称轴为x=![]() ,
,
①如图2,当CD1∥AB时,四边形ACD1B为梯形,
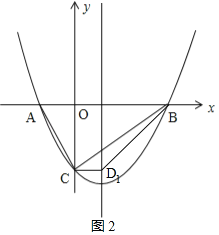
∵点C(0,﹣2),
∴点D1坐标为(![]() ,﹣2);
,﹣2);
②如图3,当AD2∥BC时,四边形ACBD2为梯形,

∴∠D2AE=∠CBO,
∵∠AED2=∠BOC=90°,
∴△AD2E∽△BOC,
∴![]() ,即
,即![]() ,
,
解得:D2E=![]() ,
,
∴点D2坐标为(![]() ,
,![]() );
);
③如图4,当BD3∥AC时,四边形ACBD3为梯形,
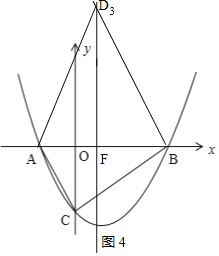
∴∠OAC=∠FBD3,
∵∠AOC=∠BFD3=90°,
∴△AOC∽△BFD3,
∴![]() ,即
,即![]() ,
,
解得:FD3=3,
∴点D3的坐标为(![]() ,3);
,3);
综上,点D的坐标为(![]() ,﹣2)或(
,﹣2)或(![]() ,
,![]() )或(
)或(![]() ,3).
,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
材料1:数学上有一种根号内又带根号的数,它们能通过完全平方式及二次根式的性质化去一层(或多层)根号.如:
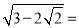
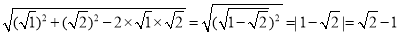 ;
;材料2: 配方法是初中数学思想方法中的一种重要的解题方法。配方法的最终目的就是配成完全平方式,利用完全平方式来解决问题。它的应用非常广泛,在解方程、求最值、证明等式、化简根式、因式分解等方面都经常用到。
如:
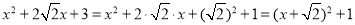
∵
 ,∴
,∴ 即
即
∴
 的最小值为1.
的最小值为1.根据以上材料解决下列问题:
(1)填空:
 =________________;
=________________;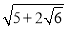 =______________;
=______________;(2)求
 的最小值;
的最小值;(3)已知
 ,求
,求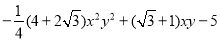 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:矩形ABCD中,AB=4,BC=3,点M、N分别在边AB、CD上,直线MN交矩形对角线 AC于点E,将△AME沿直线MN翻折,点A落在点P处,且点P在射线CB上.
(1)如图1,当EP⊥BC时,求CN的长;
(2) 如图2,当EP⊥AC时,求AM的长;
(3) 请写出线段CP的长的取值范围,及当CP的长最大时MN的长.
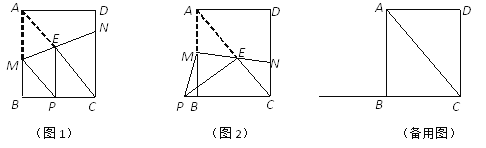
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠B=60,E是边CD上一点,以CE为边作等边△CEF.
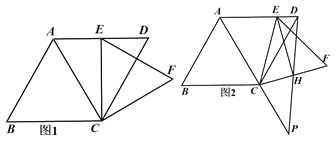
(1) 如图1,当CE⊥AD ,CF=
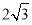 时,求菱形ABCD的面积;
时,求菱形ABCD的面积;(2) 如图2,过点E作∠CEF的平分线交CF于H,连接DH,并延长DH与AC的延长交于点P,若∠ECD=15,求证:
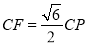 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
-
科目: 来源: 题型:
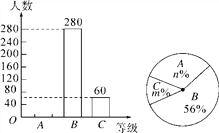
查看答案和解析>>【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)这次调查的市民人数为________人,m=________,n=________;
(2)补全条形统计图;
(3)若该市约有市民100000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
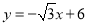 与x轴、y轴分别交于A、B两点,C点坐标是(0,2),连接AC.
与x轴、y轴分别交于A、B两点,C点坐标是(0,2),连接AC.
(1)直接写出A、B两点的坐标:A(______,_____)、B(_____,_____);
(2)在AB上找一点P,当PC+PO最小时,在AC上找一点Q使得PQ+
 最小,求Q点坐标;
最小,求Q点坐标;(3)在(2)的条件下,平面内能否找到一点K,使得点A、C、P、K构成的四边形是平行四边形,若能,直接写出K点坐标,若不能,请说明理由.
相关试题

