【题目】如图,已知![]() ,
,![]() ,
,![]() 平分
平分![]() ,即
,即![]() ,
,![]() 平分
平分![]() ,即
,即![]() ;
;
![]() 若
若![]() ,则
,则![]() ________;
________;
![]() 若
若![]() 可以在
可以在![]() 内部绕点
内部绕点![]() 作任意旋转(射线
作任意旋转(射线![]() 与射线
与射线![]() 不重合,射线
不重合,射线![]() 与射线
与射线![]() 不重合)则
不重合)则![]() 的大小是否改变?试说明理由.
的大小是否改变?试说明理由.
参考答案:
【答案】(1)![]() ;(2)不改变.
;(2)不改变.
【解析】
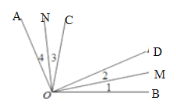
(2)由图形可知∠AOC=∠AOB-∠COD-∠BOD,由∠AOB=120°,∠COD=50°,∠BOD=30°,可得∠AOC的度数,再根据角平分线的定义可得∠2=![]() ∠BOD,∠3=
∠BOD,∠3=![]() ∠AOC,再利用∠MON=∠COD+∠2+∠3,即可求得∠MON的度数;
∠AOC,再利用∠MON=∠COD+∠2+∠3,即可求得∠MON的度数;
(2)由题意知∠AOC+∠BOD=∠AOB-∠COD=120°-50°=70°,根据角平分线的定义可得∠2=![]() ∠BOD,∠3=
∠BOD,∠3=![]() ∠AOC,所以∠2+∠3=
∠AOC,所以∠2+∠3=![]() (∠AOC+∠BOD)=35°,故可得∠MON=∠COD+∠2+∠3=50°+35°=85°,故∠MON的大小不会改变.
(∠AOC+∠BOD)=35°,故可得∠MON=∠COD+∠2+∠3=50°+35°=85°,故∠MON的大小不会改变.
(1)∵∠AOB=120°,∠COD=50°,∠BOD=30°,
∴∠AOC=120°-50°-30°=40°,
∵OM平分∠BOD,即∠1=∠2,ON平分∠AOC,即∠3=∠4,
∴∠2=15°,∠3=20°,
∴∠MON=∠COD+∠2+∠3=50°+15°+20°=85°,
故答案为:85°;
(2)不改变,理由:
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,即
,即![]() ,
,![]() 平分
平分![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故不改变.
-
科目: 来源: 题型:
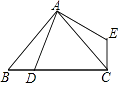
查看答案和解析>>【题目】如图,已知点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连AD,线段AD绕点A逆时针方向旋转90°得到线段AE,连CE,求证:BD⊥CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=
 .其中正确的是________(填序号).
.其中正确的是________(填序号).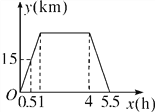
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2 .
(1)求k的取值范围;
(2)试说明x1<0,x2<0;
(3)若抛物线y=x2﹣(2k﹣3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OAOB﹣3,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解答问题.
材料:将一组正整数1,2,3,4,5,…按下面的方法进行排列:

我们规定:正整数2的位置记为(1,2),正整数8的位置记为(2,5).
问题:(1)若一个数a的位置记作(4,3),则a=________;
(2)正整数2017的位置可记为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 为直线
为直线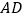 上一点,以
上一点,以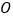 为顶点作
为顶点作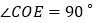 ,射线
,射线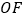 平分
平分 .
.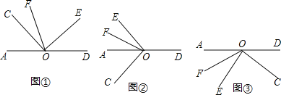
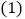 如图①,
如图①,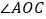 与
与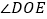 的数量关系为________,
的数量关系为________,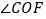 和
和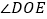 的数量关系为_________;
的数量关系为_________;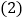 若将
若将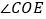 绕点
绕点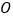 旋转至图②的位置,
旋转至图②的位置,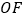 依然平分
依然平分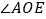 ,请写出
,请写出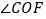 和
和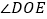 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;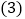 若将
若将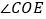 绕点
绕点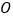 旋转至图③的位置,射线
旋转至图③的位置,射线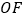 依然平分
依然平分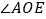 ,请直接写出
,请直接写出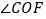 和
和 之间的数量关系.
之间的数量关系.
相关试题

