【题目】如图,已知点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连AD,线段AD绕点A逆时针方向旋转90°得到线段AE,连CE,求证:BD⊥CE. 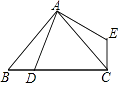
参考答案:
【答案】证明:∵△ABC为等腰直角三角形, ∴∠B=∠ACB=45°,
∵线段AD绕点A逆时针方向旋转90°得到线段AE,
∴∠ACE=∠B=45°,
∴∠ACB+∠ACE=45°+45°=90°,即∠BCE=90°,
∴BD⊥CE.
【解析】根据等腰直角三角形的性质得∠B=∠ACB=45°,再根据旋转的性质得∠ACE=∠B=45°,则∠ACB+∠ACE=90°,于是可判断BD⊥CE.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=30 cm,BC=35 cm,∠B=60°,有一动点M自A向B以1 cm/s的速度运动,动点N自B向C以2 cm/s的速度运动,若M,N同时分别从A,B出发.
(1)经过多少秒,△BMN为等边三角形;
(2)经过多少秒,△BMN为直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=
 .其中正确的是________(填序号).
.其中正确的是________(填序号).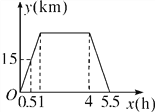
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?

-
科目: 来源: 题型:
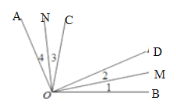
查看答案和解析>>【题目】如图,已知
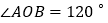 ,
, ,
,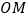 平分
平分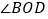 ,即
,即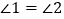 ,
,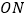 平分
平分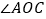 ,即
,即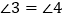 ;
;
 若
若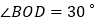 ,则
,则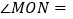 ________;
________;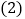 若
若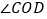 可以在
可以在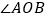 内部绕点
内部绕点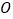 作任意旋转(射线
作任意旋转(射线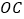 与射线
与射线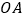 不重合,射线
不重合,射线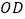 与射线
与射线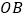 不重合)则
不重合)则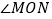 的大小是否改变?试说明理由.
的大小是否改变?试说明理由.
相关试题

