【题目】如图,OD平分∠BOC,OE平分∠AOC,∠BOC=60°,∠AOC=58°.
(1)求出∠AOB及其补角的度数;
(2)①请求出∠DOC和∠AOE的度数;
②判断∠DOE与∠AOB是否互补,并说明理由.

参考答案:
【答案】(1)118°;62°(2)①29°②不互补
【解析】
(1)由∠AOB=∠BOC+∠AOC可求出∠AOB的度数,进而求出其补角的度数.
(2)①由OD和OE是∠BOC和∠AOC的平分线可求出∠DOC和∠AOE的度数.
②由∠DOE=∠DOC+∠COE可知∠DOE的度数,计算∠AOB与∠DOE的和即可判断∠AOB与∠DOE是否为补角.
(1)∠AOB=∠BOC+∠AOC=60°+58°=118°,
其补角为180°-∠AOB=180°-118°=62°.
(2)①因为OD平分∠BOC,OE平分∠AOC,
所以∠DOC=∠BOD=![]() ∠BOC=
∠BOC=![]() ×60°=30°,∠AOE=∠COE=
×60°=30°,∠AOE=∠COE=![]() ∠AOC=
∠AOC=![]() ×58°=29°.
×58°=29°.
②∠DOE与∠AOB不互补.
理由:因为∠DOC=30°,∠COE=29°,
所以∠DOE=∠DOC+∠COE=59°.
所以∠DOE+∠AOB=59°+118°=177°,![]()
故∠DOE与∠AOB不互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆自行车,前胎行驶6000km就不能继续使用,后胎行驶4000km就不能继续使用,若在行驶中合理交换前后胎,则最多可以行驶_____km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c过原点O、点A (2,﹣4)、点B (3,﹣3),与x轴交于点C,直线AB交x轴于点D,交y轴于点E.
(1)求抛物线的函数表达式和顶点坐标;
(2)直线AF⊥x轴,垂足为点F,AF上取一点G,使△GBA∽△AOD,求此时点G的坐标;
(3)过直线AF左侧的抛物线上点M作直线AB的垂线,垂足为点N,若∠BMN=∠OAF,求直线BM的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )
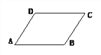
A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,矩形ABCD中,BD=5cm,BC=4cm,E是边AD上一点,且BE = ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF + PG的长为( ).

A. 2.5 cm B. 2.8 cm C. 3 cm D. 3.5 cm
-
科目: 来源: 题型:
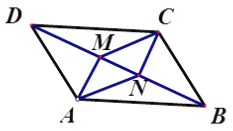
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AM、CN都是BD的垂线,M、N是垂足.
求证:(1)AM=CN;(2)∠MAN=∠NCM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
x+6与y轴交于点A,与x轴交于点B,点M是射线AB上一动点(点M不与点A、B重合),以点M为圆心,MA长为半径的圆交y轴于另一点C,直线MC与x轴交于点D,点E是线段BD的中点,射线ME交⊙M于点F,连接OF.
(1)若MA=2,求C点的坐标;
(2)若D点的坐标为(4,0),求MC的长;
(3)当OF=MA时,直接写出点M的坐标.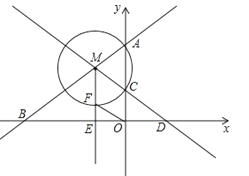
相关试题

