Question

【题目】如图，抛物线y=ax2+bx+c过原点O、点A （2，﹣4）、点B （3，﹣3），与x轴交于点C，直线AB交x轴于点D，交y轴于点E．
（1）求抛物线的函数表达式和顶点坐标；
（2）直线AF⊥x轴，垂足为点F，AF上取一点G，使△GBA∽△AOD，求此时点G的坐标；
（3）过直线AF左侧的抛物线上点M作直线AB的垂线，垂足为点N，若∠BMN=∠OAF，求直线BM的函数表达式．

Answer 1

【答案】解：（1）∵将原点O、点B、点C的坐标代入得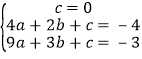：，解得：a=1，b=﹣4，c=0，
∴抛物线的解析式为y=x2﹣4x．
（2）设直线AB的解析式为y=kx+b．
∵将点A（2，﹣4）、B（3，﹣3）代入得，解得：k=1，b=﹣6，
∴直线AB的解析式为y=x﹣6．
∵令y=0得x﹣6=0，解得：x=6，
∴D（6，0）．
∴OD=6．
∵AF⊥x轴，（2，﹣4），
∴F（2，0）．
∴AF=4，DF=4．
∴AF=DF．
∴∠GAB=∠ODA．
∴当时，△GBA∽△AOD．
∵由两点间的距离公式可知AB==，AD==4，
∴，解得；AG=．
∴G（2，﹣）．
（3）如图1所示：BM与AF的交点记为G．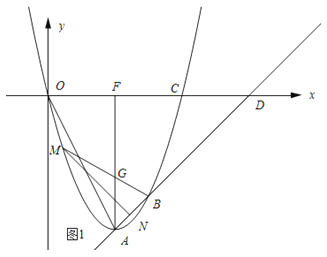

∵∠BMN=∠OAF，∠A=∠ODA，
∴△GBA∽△AOD．
∴，即，解得；AG=．
∴G（2，﹣）．
设直线BM的解析式为y=kx+b．
∵将点B、G的坐标代入得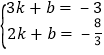：，解得：k=﹣，b=﹣2．
∴直线BM的解析式为y=﹣X﹣2．
如图2所示：MB与x交点记为G．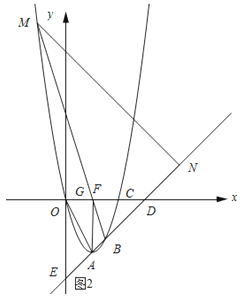

BD=AD﹣AB=4﹣=3．
∵∠BMN=∠OAF，∠GDB=∠ODA，
∴△FBD∽△AOD．
∴，即，解得DG=4．
∴点G的坐标为（2，0）．
设直线BM的解析式为y=kx+b．
∵将点B和点G的坐标代入得：，解得k=﹣3，b=6．
∴直线BM的解析式为y=﹣3x+6．
综上所述，直线MB的解析式为y=-x﹣2或y=﹣3x+6．
【解析】（1）将原点O、点B、点C的坐标代入求得a、b、c的值即可；
（2）先求得直线AB的解析式，然后可求得点D的坐标，于是得到AF=DF，由两点间的距离公式可求得AB、AD的长，由等腰三角形的性质可证明∠GAB=∠ODA，故此时，△GBA∽△AOD．接下来依据关系式可求得AG的长，从而可求得点G的坐标；
（3）如图1所示：BM与AF的交点记为G．先证明△GBA∽△AOD，由相似三角形的性质可求得AG的长，于是得到点G的坐标，然后依据待定系数法可求得BM的解析式；如图2所示：MB与x交点记为G．先证明△FBD∽△AOD，由相似三角形的性质可求得DG的长，从而得到点G的坐标，然后依据待定系数法可求得MB的解析式