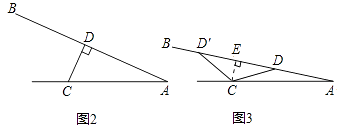
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm. 
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号) (参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.46,sin12°≈0.20)
参考答案:
【答案】
(1)解:∵∠BAC=24°,CD⊥AB,
∴sin24°= ![]() ,
,
∴CD=ACsin24°=30×0.40=12cm;
∴支撑臂CD的长为12cm
(2)解:过点C作CE⊥AB,于点E,
当∠BAC=12°时,
∴sin12°= ![]() =
= ![]() ,
,
∴CE=30×0.20=6cm,
∵CD=12,
∴DE= ![]() ,
,
∴AE= ![]() =12
=12 ![]() cm,
cm,
∴AD的长为(12 ![]() +6
+6 ![]() )cm或(12
)cm或(12 ![]() ﹣6
﹣6 ![]() )cm.
)cm.
【解析】(1)利用锐角三角函数关系得出sin24°= ![]() ,进而求出即可;(2)利用锐角三角函数关系得出sin12°=
,进而求出即可;(2)利用锐角三角函数关系得出sin12°= ![]() ,进而求出DE,AE的长,即可得出AD的长.
,进而求出DE,AE的长,即可得出AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
①若AD是∠BAC的平分线,则∠_______=∠_______=
 ∠________;
∠________;②若AE=CE,则BE是AC边上的___________________;
③若CF是AB边上的高,则∠____=∠______=90°,CF__________AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家环保局统一规定,空气质量分为5级.当空气污染指数达0﹣50时为1级,质量为优;51﹣100时为2级,质量为良;101﹣200时为3级,轻度污染;201﹣300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如图两幅不完整的统计图.请根据图中信息,解答下列各题:
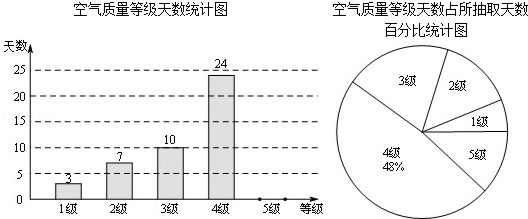
(1)本次调查共抽取了天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为°;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天) -
科目: 来源: 题型:
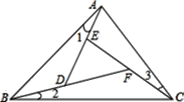
查看答案和解析>>【题目】在学完三角形的内、外角后,教师要求同学们根据所学的知道设计一个利用“三角形一个外角等于与它不相邻的两个内角的和”求解的问题.如图:在△ABC中,∠1=∠2=∠3.
(1)试说明:∠BAC=∠DEF;
(2)若∠BAC=70°,∠DFE=50°,求∠ABC度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴n=3,m=﹣3
(1)若x2+2y2﹣2xy+4y+4=0,求xy的值
(2)已知△ABC的三边长a,b,c都是正整数,且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0,请问△ABC是怎样形状的三角形?
(3)根据以上的方法是说明代数式:x2+4x+y2﹣8y+21的值一定是一个正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是,车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中②的位置).例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.
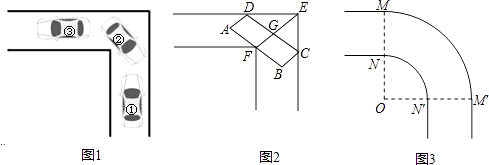
(1)小平认为长8m,宽3m的消防车不能通过该直角转弯,请你帮他说明理由;
(2)小平提出将拐弯处改为圆弧(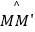 和
和 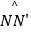 是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子?
是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①单项式-
 的系数为-
的系数为- ,次数为2;②90°的角叫余角,180°的角叫补角③若AC=BC,则点C是线段AB的中点;④经过一点有且只有一条直线与这条直线平行,其中错误的说法有( )
,次数为2;②90°的角叫余角,180°的角叫补角③若AC=BC,则点C是线段AB的中点;④经过一点有且只有一条直线与这条直线平行,其中错误的说法有( )A. 1个 B. 2个 C. 3个 D. 4个
相关试题

