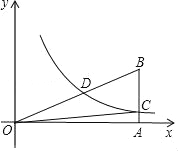
【题目】若关于x的一元二次方程x2+(2k﹣1)x+k2=0的两根a、b满足a2﹣b2=0,双曲线![]() (x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
(x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
A. 3 B. ![]() C. 6 D. 3或
C. 6 D. 3或![]()
参考答案:
【答案】B
【解析】
首先由一元二次方程根的判别式得出k的取值范围,然后由a2﹣b2=0得出a+b=0或a-b=0,再运用一元二次方程根与系数的关系求出k的值,由k的几何意义,可知S△OBA=![]()
![]() .如果过D作DE⊥OA于E,则S△OCA=
.如果过D作DE⊥OA于E,则S△OCA=![]()
![]() .易证△ODE∽△OBA,根据相似三角形的面积比等于相似比的平方,得出S△OBA,最后由S△OBC=S△OBA-S△OCA,得出结果.
.易证△ODE∽△OBA,根据相似三角形的面积比等于相似比的平方,得出S△OBA,最后由S△OBC=S△OBA-S△OCA,得出结果.
∵x2+(2k-1)x+k2=0有两根,
∴△=(2k-1)2-4k2≥0,
即k≤![]() .
.
由a2﹣b2=0得:(a-b)(a+b)=0.
当a+b=0时,-(2k-1)=0,解得k=![]() ,不合题意,舍去;
,不合题意,舍去;
当a-b=0时,a=b,△=(2k-1)2-4k2=0,
解得:k=![]() 符合题意.
符合题意.
∵![]() ,
,
∴双曲线的解析式为:![]() .
.
过D作DE⊥OA于E,则S△ODE=S△OCA=![]() ×1=
×1=![]() .
.
∵DE⊥OA,BA⊥OA,
∴DE∥AB,∴△ODE∽△OBA,
∴![]() ,∴S△OBA=4×
,∴S△OBA=4×![]() =2,
=2,
∴S△OBC=S△OBA-S△OCA=2-![]() =
=![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
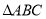 中,
中,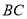 的垂直平分线
的垂直平分线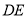 交
交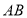 于点
于点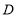 ,交
,交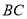 于点
于点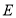 .
.(1)如图1,若
 ,
,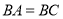 ,
,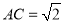 ,求
,求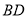 的长;
的长;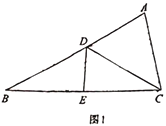
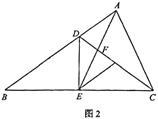
(2)如图2,连接
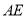 交
交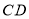 于点
于点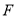 ,若
,若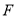 为
为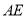 的中点,且满足
的中点,且满足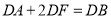 ,求证:
,求证: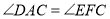 .
.
-
科目: 来源: 题型:
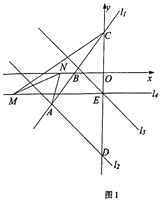
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
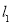 :
: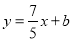 与直线
与直线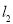 :
: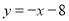 交于点
交于点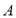 ,已知点
,已知点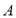 的横坐标为-5,直线
的横坐标为-5,直线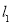 与
与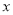 轴交于点
轴交于点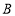 ,与
,与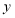 轴交于点
轴交于点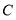 ,直线
,直线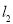 与
与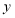 轴交于点
轴交于点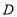 .
.
(1)求直线
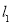 的解析式;
的解析式;(2)将直线
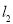 向上平移6个单位得到直线
向上平移6个单位得到直线 ,直线
,直线 与
与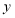 轴交于点
轴交于点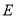 ,过点
,过点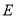 作
作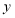 轴的垂线
轴的垂线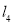 ,若点
,若点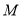 为垂线
为垂线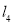 上的一个动点,点
上的一个动点,点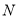 为
为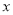 轴上的一个动点,当
轴上的一个动点,当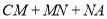 的值最小时,求此时点
的值最小时,求此时点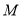 的坐标及
的坐标及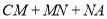 的最小值;
的最小值;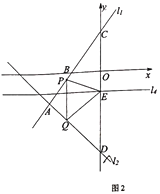
(3)已知点
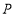 、
、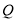 分别是直线
分别是直线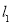 、
、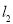 上的两个动点,连接
上的两个动点,连接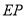 、
、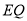 、
、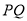 ,是否存在点
,是否存在点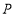 、
、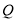 ,使得
,使得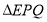 是以点
是以点 为直角顶点的等腰直角三角形,若存在,求点
为直角顶点的等腰直角三角形,若存在,求点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.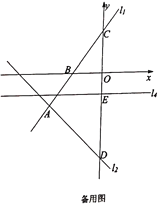
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线
 经过点
经过点 ,直线
,直线 经过点
经过点 ,且
,且 与
与 关于
关于 轴对称,则
轴对称,则 与
与 的交点坐标为( )
的交点坐标为( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是函数y=
 图象上的一点,已知B(﹣
图象上的一点,已知B(﹣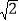 ,﹣
,﹣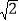 ),C(
),C(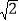 ,
,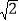 ).试利用性质:“y=
).试利用性质:“y= 图象上的任意一点P都满足|PB﹣PC|=2
图象上的任意一点P都满足|PB﹣PC|=2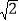 ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y= 图象上运动时,点F也总在一图形上运动,该图形为( )
图象上运动时,点F也总在一图形上运动,该图形为( )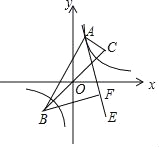
A. 圆 B. 双曲线 C. 抛物线 D. 直线
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=
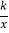 (k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为
(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为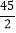 ,则k的值为_____.
,则k的值为_____.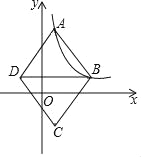
相关试题

